统招专升本高数一考试模拟试卷(一)
考试总分:100分
考试类型:模拟试题
作答时间:120分钟
已答人数:924
试卷答案:没有
试卷介绍: 统招专升本高数一考试模拟试卷已经整理好,需要备考的朋友们赶紧来刷题吧!
试卷预览
-
1. 函数
 的定义域是()
的定义域是()
A[-4,3]
B[-4,2]
C(2,3]
D(-4,3)
-
2. 已知du(x,y)=[axy3+cos(x+2y)]dx+[3x2y2+bcos(x+2y)]dy,且u(x,y)具有二阶连续偏导数.则()
Aa=2,b=-2
Ba=3,b=2
Ca=2,b=2
Da=-2,b=2
-
3. 设函数z=ln(3x2y3),则
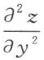 =()
=()
A
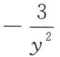
B
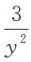
C
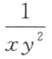
D

-
4. 已知f(xy,x-y)=x2+y2,则
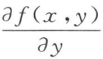 =()
=()
A2
B2x
C2y
D2x+2y
-
5. 设三元函数u=xy+ycosx+3zy,则
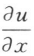 =()
=()
Ay-ysinx
Bx+ysinx
Cy-cosx
Dy+ysinx
-
6. 函数
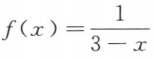 在(-3,3)内展开成x的幂级数是()
在(-3,3)内展开成x的幂级数是()
A

B

C
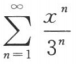
D
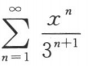
-
7. 设函数f(u)连续,区域D={(x,y)|x2+y2≤2y},则
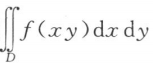 =()
=()
A
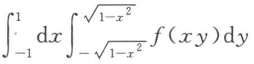
B
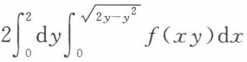
C
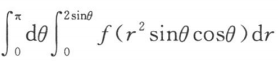
D
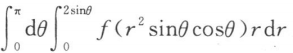
-
8. 曲面z=F(2x,y,2z)在点(x,y,z)处切平面的法向量为()
A{2Fx,Fy,2Fz-1}
B{2Fx,Fy-1,2Fz-1}
C{Fx,Fy,2Fz}
D{-2Fx,-2Fy,1}
-
9. 平面π1:x-2y+2z-2=0和平面π2:2x-2y+3=0的夹角为()
A
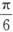
B

C
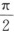
D
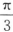
-
10. 若函数y=f(x)满足f′(x0)=
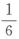 ,则当△x→0时,该函数在点x=x0处的微分dy是()
,则当△x→0时,该函数在点x=x0处的微分dy是()
A与△x等价的无穷小
B与△x同阶非等价的无穷小
C比△x低阶的无穷小
D比△x高阶的无穷小
-
11. x=0为函数f(x)=
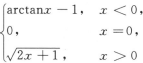 的___间断点.()
的___间断点.()
A跳跃
B可去
C振荡
D无穷
-
12. 当x→a,f(x)为___时,必有
 (x-a)f(x)=0.()
(x-a)f(x)=0.()
A有界函数
B任意函数
C单调函数
D无界函数
-
13. 设两个函数f(x)及g(x)都在点x=a处取得极大值,则函数F(x)=f(x)g(x)在点x=a处()
A必取极大值
B必取极小值
C不可能取极值
D是否取极值不能确定
-
14. 下列积分中,积分结果正确的是()
A

B
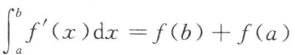
C

D
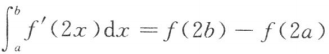
-
15. ∫arcsinxdx=()
Aarcsinx+
 +C
+CBxarcsinx+
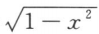 +C
+CCarcsinx-
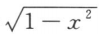 +C
+CDxarcsinx-
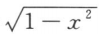 +C
+C
-
1. 设f(x,y)=x2+y2-exy,则f(2,0)=().
-
2. 满足方程y”=x,且在点(0,1)处的切线方程为
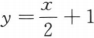 的曲线方程为().
的曲线方程为().
-
3. 设函数y=ae-x+be5x是某个二阶微分方程满足初始条件
 的特解,ab为常数,则a=(),b=().
的特解,ab为常数,则a=(),b=().
-
4. 函数
 展开成x的幂级数为().
展开成x的幂级数为().
-
5. 幂级数
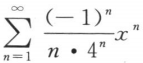 的收敛域为().
的收敛域为().
-
6. 已知y=
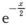 cos3x,则y′=().
cos3x,则y′=().
-
7. 设f(x)=
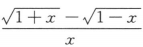 ,则补充定义f(0)=()时,函数f(x)在点x=0处连续.
,则补充定义f(0)=()时,函数f(x)在点x=0处连续.
-
8. 已知函数f(x)=
 在x=0处的极限存在,则a=().
在x=0处的极限存在,则a=().
-
9. 已知y=y(x)是由方程xy=ey-x确定的函数,则dy=().
-
10. 若f(x)>3,且在区间[0,2]上连续,则函数F(x)=2x+5-
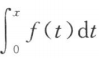 在区间[0,2]上单调().(填“递增”或“递减”)
在区间[0,2]上单调().(填“递增”或“递减”)
-
1. 设z=f(u),f(u)可导,u=3x2y+
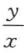 ,求
,求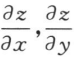 .
.
-
2. 求z=ln(x+y)的全部二阶偏导数.
-
3. 求下列方程所表示的球面的球心和半径: (1)x2+y2+z2+2x-4y+3z+
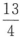 =0;(2)2x2+2y2+2z2-z=0.
=0;(2)2x2+2y2+2z2-z=0.
-
4. 设
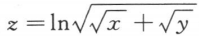 ,求证:
,求证: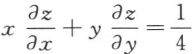 .
.
-
5. 问函数
 在点P(1,2,1)处沿什么方向的方向导数最大?并求出此方向导数的最大值.
在点P(1,2,1)处沿什么方向的方向导数最大?并求出此方向导数的最大值.
-
6. 计算
 .
.
-
7. 求通过x轴和点M(4,-3,-1)的平面方程.
-
8. 已知当x→0时,有ln(cos
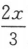 )~Axk,求常数A和k的值.
)~Axk,求常数A和k的值.
-
9. 已知
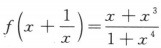 ,求f(x).
,求f(x).
-
10. 判断以M1(4,3,1)、M2(7,1,2)、M3(5,2,3)三点为顶点的三角形是一个怎样的特殊三角形.
-
11. 计算不定积分
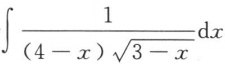 .
.
-
12. 求不定积分
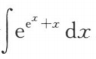 .
.
-
13. 设f(x)在[a,b]上有连续,在(a,b)内可导,b-a≥4,求证:存在一点ξ∈(a,b),使得f"(ξ)<f2(ξ).
-
14. 设函数f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b),证明:若f(x)不恒为常数,则至少存在一点ξ∈(a,b),使得f′(ξ)>0.
-
15. 求方程y”-2y'-3y=3x+1的一个特解.