对f(x, y)=0 隐函数求导时,把x当作中间变量看。( )
查看答案
相关试题
换一换


对f(x, y)=0 隐函数求导时,把x当作中间变量看。( )
答案
已知函数f(x,y)满足fxy″=2(y+1)ex,fx′(x,0)=(x+1)ex,f(0,y)=y2+2y,求f(x,y)的极值。
答案
由方程F(x,y)=0确定可导函数y=y(x),称为隐函数
答案
隐函数存在的前提是函数f(x,y)在某点P0处()
A.有意义 B.函数值为零 C.可微 D.可导
答案
设函数y=f(x)在x0的自变量的改变量为ΔX,相应的函数改变量为△y,O(ΔX)表示ΔX的高阶无穷小.若函数y=f(x)在x0可微,则下列表述不正确的是( )
A.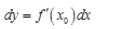 B.
B.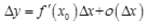 C.
C.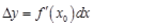 D.
D.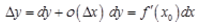
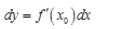 B.
B.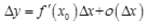 C.
C.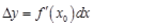 D.
D.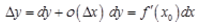
答案
约束项就是逻辑函数中不会出现的变量取值组合,用卡诺图化简时,可将约束项当作1,也可当作0()
答案
若F(x)是连续变量X的分布函数,则F(x)≥0()
答案
约束项就是逻辑函数中不允许出现的变量取值组合,用卡诺图化简时,可将约束项当作1,也可当作0()
答案
约束项就是逻辑函数中不允许出现的变量取值组合,用卡诺图化简时,可将约束项当作1,也可当作0()。
答案
若F(x)是连续变量X的分布函数,则0≤F(x)≤1()
答案
热门试题
由方程所确定的隐函数y在x=0的切线方程为()。
设随机变量X~U(0,1),在X=x(0 (1)求X,y的联合密度函数;
(2)求y的边缘密度函数.
设随机变量X ~ N(0, 1),X的分布函数为Φ(x),则P{|X| > 2} =()
设随机变量X的概率密度函数为f(x)=2x0
设函数y=y(x)是由方程cos(xy)=x+y所确定的隐函数,求函数曲线y=y(x)过点(0,1)的切线方程。
设x是整型变量,与函数IIf(x>0,-x,x)有相同结果的代数式是
设x是整型变量,与函数IIf(x<0,-x,x)有相同结果的代数式是______。
设x是整型变量,与函数Ⅱf(x>0,-x,x)有相同结果的代数式是
设随机变量X~N(0,1),则Y=|X|的密度函数为()。
设二维随机变量(X,Y)的密度函数为$f(x,y)={(1,(0≤x≤,0≤y≤1)),(0,其他):}$,则X与Y
如果函数f(x)当x→x0时极限存在,则函数f(x)在点x0处( )。
若f(x),g(x)在同一区间[a,b]上都是某随机变量的概率密度函数,证明: (1)f(x)+g(x)在[a,b]上不是随机变量的密度函数; (2)对任一常数β(0<β<1),βf(x)+(1-β)g(x)是随机变量的概率密度函数。
垂直于x轴的动直线与过原点的曲线y=y(x)(x≥0,y≥0)以及x轴围成一个以[0,x]为底边的曲边梯形,其面积为y3(x).函数y(x)的隐函数形式是()
当x→0时,变量是( )《》( )
中国大学MOOC: 若F(x)是连续变量X的分布函数,则0≤F(x)≤1.
设F(x)是随机变量X的分布函数,则对()随机变量X,有P{X₁
当随机变量X的可能值充满以下哪个区间时函数f(x)=cos(x)可以成为随机变量X的密度函数()
设随机变量X~N(0,1),X的分布函数为φ(X),则P(|X|>2)的值为()。
设随机变量X~N(0,1),X的分布函数为φ(x),则P(|X|2)的值为( )
设随机变量X~N(0,1),X的分布函数为φ(x)。则P(|X|>2)的值为()。
(2)求y的边缘密度函数.



 使用微信扫一扫登录
使用微信扫一扫登录