2025年成考高起点每日一练《数学(理)》4月23日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:1382
试卷答案:有
试卷介绍: 2025年成考高起点每日一练《数学(理)》4月23日专为备考2025年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 设集合M={x||x-2|<1},N={x|x>2},则M∩N=()
A{x|1<x<3}
B{x|x>2}
C{x|2<x<3}
D{x|1<x<2}
-
2. 一部电影在4个单位轮映,每一单位放映一场,轮映次序有()。
A4种
B16种
C24种
D256种
-
3. 若a>b>0,则()。
Alog2a
B2a<2b
C
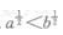
D
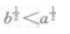
-
4.
 展开式中,末3项的系数(a,x 均未知) 之和为()
展开式中,末3项的系数(a,x 均未知) 之和为()
A22
B12
C10
D-10
-
1. 设a为实数,且tanα和tanβ是方程ax2+(2a-3)x+(a-2)=0的两个实根,求tan(α+β)的最小值。
-
2. 已知函数f(x)=(x-4)(x2-a) (I)求f"(x); (Ⅱ)若f"(-1)=8,求f(x)在区间[0,4]的最大值与最小值
-
3. 为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得
 AB=120m,求河的宽
AB=120m,求河的宽

-
4. cos20°cos40°cos80°的值。
-
1. 一个问题在1小时内,甲能独立解决的概率是0.5,乙能独立解决的概率是0.4,两人在1小时内解决问题的概率是______。
-
2.
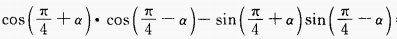 =______。
=______。
相关试卷
-
2025年成考高起点每日一练《数学(理)》2月26日359人做过
-
2025年成考高起点每日一练《数学(理)》2月27日892人做过
-
2025年成考高起点每日一练《数学(理)》2月28日1855人做过
-
2025年成考高起点每日一练《数学(理)》3月1日745人做过
-
2025年成考高起点每日一练《数学(理)》3月2日355人做过
-
2025年成考高起点每日一练《数学(理)》3月3日1478人做过
-
2025年成考高起点每日一练《数学(理)》3月4日1738人做过
-
2025年成考高起点每日一练《数学(理)》3月5日166人做过
-
2025年成考高起点每日一练《数学(理)》3月6日1136人做过
-
2025年成考高起点每日一练《数学(理)》3月7日521人做过
相关题库