单选题
1、设函数y=e-x，则y’等于（）。
答 案：C
解 析：本题考查的知识点为复合函数导数的运算 由复合函数的导数链式法则知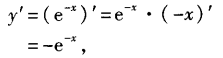
可知应选C。
2、设z=ysinx，则
等于（）。
答 案：C
解 析：本题考查的知识点为二阶偏导数。 
可知应选C。
3、直线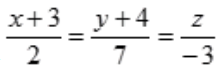
与平面4x－2y－3z－3＝0的位置关系是（）。
答 案：C
解 析：直线的方向向量s＝(2，7，－3)，且此直线过点（－3，－4，0），已知平面的法向量n＝(4,－2,－3),故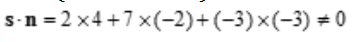
，又因点（－3，－4，0）不在已知平面内，所以已知直线相交于已知平面。
主观题
1、求微分方程y''－9y＝0的通解
答 案：解：特征方程为r2－9＝0，其特征根为r1＝-3，r2＝3，故通解为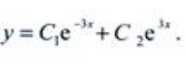
（C1，C2为任意常数）
2、计算
答 案：解：令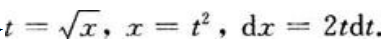
当x＝4时，t＝2；当x＝9时，t＝3。则有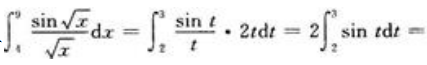
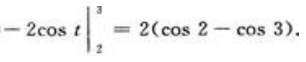
3、求微分方程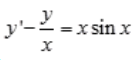
满足初始条件
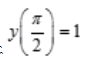的特解。
答 案：解：将方程改写为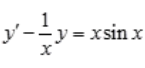
，
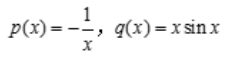，则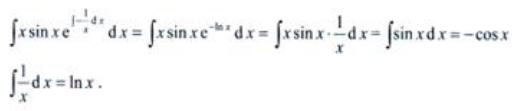
故方程通解为
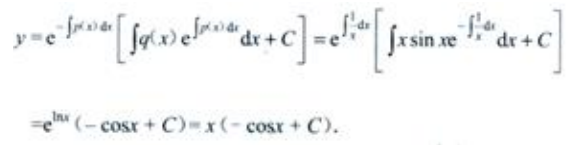将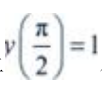
代入通解，得
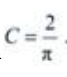从而所求满足初始条件
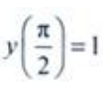的特解为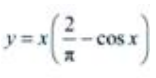
填空题
1、设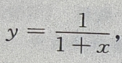
则dy=（）
答 案：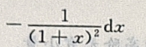
解 析：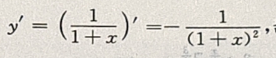
故有
2、定积分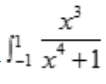
dx＝（）。
答 案：
解 析：因为
是奇函数，所以定积分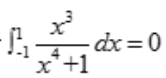
。
3、
（）。
答 案：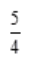
解 析：所求极限的表达式为分式，当x→2时，分母的极限不为零，因此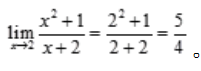
。
简答题
1、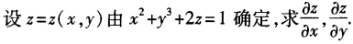
答 案：
解 析：本题考查的知识点为求二元隐函数的偏导数。 
