牛顿--莱布尼茨公式把求定积分的题转化为求 ____的函数问题
查看答案
相关试题
换一换


牛顿--莱布尼茨公式把求定积分的题转化为求 ____的函数问题
答案
下列积分中不能使用牛顿-莱布尼茨公式的是()。
A. 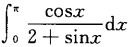 B.
B. 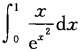 C.
C.  D.
D. 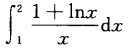
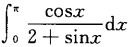 B.
B. 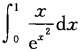 C.
C.  D.
D. 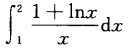
答案
下列积分可以用牛顿-莱布尼茨公式进行计算的是()
A. B.
B.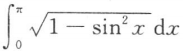 C.
C.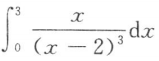 D.
D.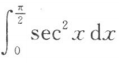
 B.
B.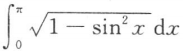 C.
C.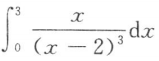 D.
D.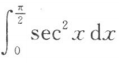
答案
中国大学MOOC: 对函数求定积分,正确的描述是:
答案
当利用int()函数求定积分时,若积分上限或下限是一个符号表达式,则该被积函数不可积
A.正确 B.错误
答案
当利用rijibi int()函数求定积分时,若积分上限或下限是一个符号表达式,则该被积函数不可积。
A.正确 B.错误
答案
称为f(x)的不定积分,它表示/ananas/latex/p/24879: 求F(x)的全部原函数。|求F(x)的全部导数。|求f(x)的全部原函数。|求f(x)的全部导数。
答案
和牛顿先后独立发明了微积分的哲学家莱布尼茨的国籍是()
A.美国 B.英国 C.奥地利 D.德国
答案
和牛顿先后独立发明了微积分的哲学家莱布尼茨的国籍是()。
答案
对一个函数先求不定积分再求微分,两者的作用抵消后只差一个常数。()
A.正确 B.错误
答案
热门试题
求线性定常系统的传递函数条件是()。
1) 求函数 的定义域 ; 2) 求函数 的定义域 ; 3) 求函数 的定义域 ; 4) 求函数 的定义域 ./ananas/latex/p/238766
在利用牛顿环求半径公式测量曲率半径时,Dm、Dn的正确测量方法是_
莱布尼茨除了和牛顿先后独立发明了微积分之外,还对的发展做出了贡献
信号流程图可以直接采用梅逊公式求系统传递函数。()
微积分基本公式把积分学中两个重要概念定积分与
牛顿和莱布尼茨已经解决无穷小的问题。()
莱布尼茨是17世纪伟大的哲学家。他先于牛顿发表了他的微积分研究成果。但是当时牛顿公布了他的私人笔记,说明他至少在莱布尼茨发表其成果的10年前就已经运用了微积分的原理。牛顿还说,在莱布尼茨发表其成果的不久前,他在给莱布尼茨的信中谈起过自己关于微积分的思想。但是事后的研究说明,在牛顿的这封信中,有关微积分的几行字几乎没有涉及这一理论的任何重要之处。因此。可以得出结论,莱布尼茨和牛顿各自独立地发明了微积分。以下()是上述论证必须假设的。
在Excel的常用函数中,求平均值函数为(),求最大值函数为()。
求余数函数是mid函数
弹性力学平面问题共有()个待求的未知函数
求最小值问题的目标函数值是各分枝函数值的下界。()
求最小值问题的目标函数值是各分枝函数值的下界( )
求余数函数是
定积分使用分部积分公式时,应将被积函数中容易凑微分的部分选作dv
目标函数可以是求min,也可以是求max。()
求般获得最好经济效益问题是求如何合理安排决策变量(即如何安排生产)使目标函数最大的问题,求最大的目标函数问题,则记为max Z;若是如何安排生产使成本是最小的问题,则记为min Z。()
MATLAB中用()函数完成矩阵的求逆运算,用()函数求矩阵的行列式。
四、分析推理(71—80题):每道题中给出一段陈述。这段陈述被假设正确的,不容置疑的。要求应试者根据这段陈述。选择一个正确答案。第71题:莱布尼茨是17世纪伟大的哲学家。他先于牛顿发表了他的微积分研究成果。但是当时牛顿公布了他的私人笔记,说明他至少在莱布尼茨发表其成果的10年前就已经运用了微积分的原理。牛顿还说,在莱布尼茨发表其成果的不久前,他在给莱布尼茨的信中谈起过自己关于微积分的思想。但是事后的研究说明,在牛顿的这封信中,有关微积分的几行字几乎没有涉及这一理论的任何重要之处。因此.可以得出结论,莱布尼茨和牛顿各自独立地发明了微积分。 以下______是上述论证必须假设的。
用一个动滑轮把重400牛顿的货物提升,所用的力是250牛顿,求这个动滑轮的机械效率。



 使用微信扫一扫登录
使用微信扫一扫登录