2022年成考高起点数学(理)考试真题及答案

• 1. 设集合M={x||x-2|＜1}，N={x|x＞2}，则M∩N=（）

  A{x|1＜x＜3}

  B{x|x＞2}

  C{x|2＜x＜3}

  D{x|1＜x＜2}

• 2. 设函数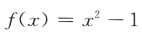，则f(x+1)=（）

  Ax²+2x+1

  Bx²+2x

  Cx²+1

  Dx²

• 3. 函数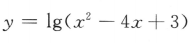的定义域是（）

  A{x|-3＜x＜-1}

  B{x|x＜-3或x＞-1}

  C{x|1＜x＜3}

  D{x|x＜1或x＞3}

• 4. 下列函数中，为奇函数的是（）

  A

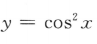
  B

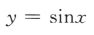
  C

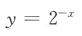
  D

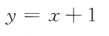
• 5. 下列函数中，为减函数的是（）

  A

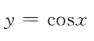
  B

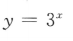
  C

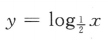
  D

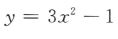
• 6. 设α是第三象限角，若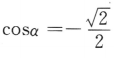，则sinα=（）

  A

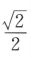
  B

  C

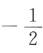
  D

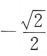
• 7. 函数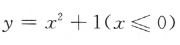的反函数是（）

  A

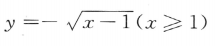
  B

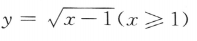
  C

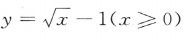
  D

• 8. 过点（-2，2）与直线x+3y-5=0平行的直线是（）

  Ax+3y-4=0

  B3x+y+4=0

  Cx+3y+8=0

  D3x-y+8=0

• 9. 已知，则sin2α=（）

  A

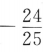
  B

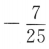
  C

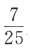
  D

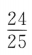
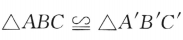• 10. 设甲：；乙：.则（）

  A甲是乙的必要条件但不是充分条件

  B甲是乙的充分条件但不是必要条件

  C甲是乙的充要条件

  D甲既不是乙的充分条件也不是乙的必要条件

• 11. 已知空间向量i,j,k为两两垂直的单位向量，向量a=2i+3j+mk，若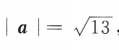，则m=（）

  A-2

  B-1

  C0

  D1

• 12. （2-3i）²=（）

  A13-6i

  B13-12i

  C-5-6i

  D-5-12i

• 13. 中心在坐标原点，对称轴为坐标轴，且一个顶点（3，0），虚轴长为8的双曲线方程是（）

  A

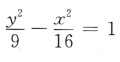
  B

  C

  D

• 14. 的展开式中，x²的系数为（）

  A20

  B10

  C5

  D1

• 15. 已知直线l：3x-2y-5=0，圆C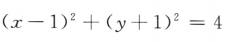：，则C上到l的距离为1的点共有（）

  A1个

  B2个

  C3个

  D4个

• 16. 袋中有6个球，其中4个红球，2个白球，从中随机取出2个球，则其中恰有1个红球的概率为（）

  A

  B

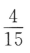
  C

  D

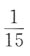
• 17. 给出下列两个命题：①如果一条直线与一个平面垂直，则该直线与该平面内的任意一条直线垂直②以二面角的棱上任意一点为端点，在二面角的两个面内分别作射线，则这两条射线所成的角为该二面角的平面角.则（）

  A①②都为真命题

  B①为真命题，②为假命题

  C①为假命题，②为真命题

  D①②都为假命题

• 1. 点(4,5)关于直线y=x的对称点的坐标为（）

• 2. 长方体的长、宽、高分别为2,3,6，则该长方体的对角线长为（）

• 3. 设函数f（x）=xsinx，则f'(x)=（）

• 4. 某校学生参加一次科技知识竞赛，抽取了其中8位同学的分数作为样本，数据如下：90,90,75,70,80,75,85,75.则该样本的平均数为（）

• 1. 在△ABC中，B=120°,BC=4,△ABC的面积为，求AC.

• 2. 已知a,b,c成等差数列，a,b,c+1成等比数列．若b=6，求a和c．

• 3. 已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
  (II）求|AB|.

• 4. 设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
  (II）求f（x）的极值．