2023年高职单招考试数学真题汇编(二)

• 1. 下面有四个语句： ①集合N*中最小的数是0； ②-a∉，则a∈N； ③a∈N，b∈，则a+b的最小值是2 ④x²+1=2x的解集中含有俩个元素. 其中说法正确的个数是（）  

  A0

  B1

  C2

  D3

• 2.  已知集合,=｛x|x²-2021x≤0｝，N=｛-1，0，1，2｝，则集合M∩N=（）  

  A{1,2}

  B{0,1,2}

  C{-1,0}

  Dφ

• 3.  已知集合M=｛x|x≥1｝，N=｛x|y=(x²-2x)｝则集合M∩N=（）  

  A∅

  B（2，+∞）

  C[2，+∞）

  D[1，2]

• 4.  下列全称量词命题与存在量词命题中： ①设A,B为俩个集合，若A∈B，则对任意x∈A, 都有x∈B ②设A，B为俩个集合，若A∉B，则存在x∈A，使得x∉B ③∀x∈{y|y是无理数}，x³是有理数； ④∀x∈{y|y是无理数}，x³是无理数。 其中真命题的个数是（）  

  A1

  B2

  C3

  D4

• 5. 已知集合A=｛（x,y）|x+y≤2，x,y∈N｝则A中元素个数为（）  

  A1

  B5

  C6

  D无数个

• 6.  一个三位数除以53，商是a，余数是b（a，b都是正整数），则a＋b的最大值是（　　）。  

  A69

  B80

  C65

  D75

• 7.  不等式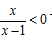的解集是（）  

  A（-∞，0）

  B(0,1)

  C(-∞,0)∪(1,+∞)

  D(1,+∞)

• 8. |x-1|>3的解集为（）  

  A（-∞，-2）

  B（-2，4）

  C（4，+∞）

  D（-∞，-2）∪（4，+∞）

• 9. 不等式x²-1>0的解集为（）  

  A{x丨x>1}

  B{x丨x<-1}

  C{x丨0

  D{x丨x<-1或x>1}

• 10.  已知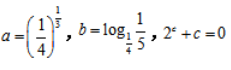，则()  

  Aa

  Bc

  Cc

  Da

• 11.  函数f（x）=e^x-2-2的零点所在的区间是（）  

  A(0,1)

  B(1,2)

  C(2,3)

  D(3,4)

• 12.  下列函数中，即是奇函数又在定义域内递增的是（）  

  Af(x)=e^x-e^-x

  Bf(x)=2^x+2^-x

  Cf(x)=

  Df(x)=ln|x|

• 13. 设alog₃4=2,则4^-a=（   ）  

  A1/16

  B1/9

  C1/8

  D1/6

• 14. 若a为实数，且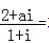3+i，则a=（    ）  

  A﹣4

  B﹣3

  C3

  D4

• 15.  将函数f(x)=2sin(x+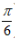)的图像上各点横坐标伸长到原来的2倍（纵坐标不变），再将所得图象向左平移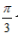个单位长度，得到函数y=g(x)的图象，则（）  

  Ag（x）=2sin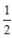x

  B

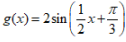
  C

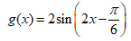
  D

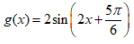
• 16. 已知某几何体的三视图如图所示，则该几何体的表面积为  

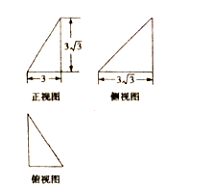
  A

  B27

  C27√2

  D27√3

• 17. ∧ABC的内角A、B、C的对边分别为a、b、c.已知a=√5，C=2，cosA=  

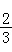
  A√2

  B√3

  C2

  D3

• 18.  某同学从6岁到12岁的年龄与身高的折线图如图所示，根据折线图，下列说法正确的是（）  

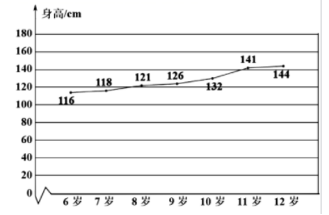
  A9岁到10岁的身高增长速度最快

  B从6岁到12岁，每年身高平均增长了5cm

  C7岁时，该同学的身高就超过了120cm

  D9岁到12岁比6岁到9岁的身高增长速度更快

• 19. 设Sn是数列｛an｝的前n项和，若Sn=n²+2n,则a₂₀₂₁=()  

  A4043

  B4042

  C4041

  D2021

• 20.  找规律填数字是一个很有趣的活动，特别锻炼观察和思考能力。下列选项中，填入数列“1、3、6、11、（ ）、32”空缺处的数字，正确的是（ ）。  

  A18

  B19

  C20

  D21'

• 21.  已知正项等比数列｛a_n｝的前n项数和为,S₃=7,则a₆=（）  

  A32

  B24

  C16

  D8

• 22.  下列命题正确的是 （）  

  A棱柱的侧面都是长方形

  B棱柱的所有面都是四边形

  C棱柱的侧棱不一定相等

  D—个棱柱至少有五个面

• 23.  已知向量AB=（2，4），BC=（4，3），那么AC=（）  

  A（6，7）

  B（2，-1）

  C（-2，1）

  D（7，6）

• 24.  在区间[0,2]上随机取一个实数x，则事件“3x-1＜0”发生的概率为()  

  A

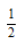
  B

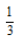
  C

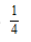
  D

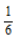
• 25. 从分别写有1，2，3，4，5的5张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为（　　）  

  A1/10

  B1/5

  C3/10

  D2/5

• 26. 已知函数f(x)的定义域为R，对任意实数a,b，如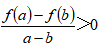，则f(x)为（）  

  A增函数 

  B减函数

  C先增后减的函数 

  D无法确定 

• 27. 已知函数式f(x)是奇函数，当x>0时，f(x)=x²+2x,则f(-1)的值为（）  

  A-3

  B-1

  C1

  D3

• 28. 函数（）  

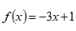  A在（0，+∞）上是增函数

  B在（-∞，0）上是增函数

  C在（-∞，+∞）上是增函数

  D在（-∞，+∞）上是减函数

• 29.  用印有“1”“5”“6”的三张卡片，可以组成许多不同的三位数，所有这些三位数的和为（　　）。

  A5992

  B5993

  C5994

  D5985

• 30. 在等差数列｛an｝中，若a₂=4,a₄=2则a₆=()  

  A-1

  B0

  C1

  D6

• 1. 已知角α的终边经过一点P(-3,4)，则sinα的值为______  

• 2. sin 120°=（）,cos 150°=（）,tan 300°=（）.

• 3. 设全集U={1,2,3,4,5,6},集合A={1,3,5},B={2,4},用集合A和集合B表示全集U,则（）。

• 4. 某中学高一班有学生50人，如果参加数学小组的有25人，参加物理小组的有32人，那么既参加数学小组，又参加物理小组的人数的最大值是______，最小值是_______.  

• 5. 已知函数f(x)是定义在R上的奇函数，当x∈ (-∞，0)时，f (x) =2x³+x²,所以f(2) =（）  

• 6. 函数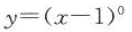的定义域为().

• 7. 已知向量a=（m,4），b=（3，-2），且a∥b,则m=（）。  

• 8. 圆锥底面的半径为5cm，高为12cm，则圆锥的侧面积为_____cm²。  

• 9. 生产某种零件，出现次品的概率是0.04，现生产这种零件4件，恰好出现一件次品的概率是________.

• 10. 1个口袋内有带标号的7个白球，3个黑球，事件A:“从袋中摸出1个是黑球，放回后再摸1个是白球”的概率是________.

• 1. 若a＜b＜0，则ab＜0。（）  

  A对

  B错

• 2. 已知函数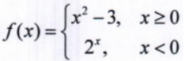，则f（1）=-2。（）

  A对

  B错

• 3. y=-x³是偶函数。（）  

  A对

  B错

• 4. 将函数y=cosx的图像沿x轴方向向左平移1个单位，便得到函数y=cos(x+1)的图像。（）  

  A对

  B错

• 5. 过已知直线外一点只能作一条直线与已知直线平行。（）  

  A对

  B错

• 1. 证明：函数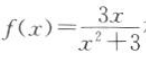在R上是奇函数.

• 2. 已知三个不等式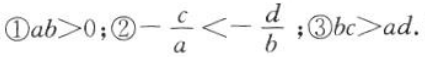：以其中两个作为条件，余下一个作为结论，可以组成多少个正确的命题?

• 3. 比较(x²+2)²与x⁴+x²+3的大小.

• 4. 已知集合(a为常数).
  (1)若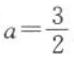,求A∩B;
  (2)若,求实数a的取值范围.

• 5. 若A,B均为锐角，且  

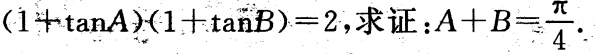
• 6. 已知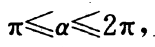且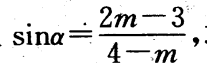求m的取值范围。  

• 7. 成等差数列的四个数的和为26,第二个数与第三个数之积为40,求这四个数.  

• 8. 三个数成等差数列，他们的和是18，他们的平方和116，求这三个数。  

• 9. 已知圆C与y轴相切，圆心C在直线x-3y=0上，且被直线y=x截得弦长为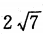，求圆C的方程.  

• 10. 如图，已知电路中4个开关闭合的概率是1/2，且是相互独立的，求灯亮的概率.

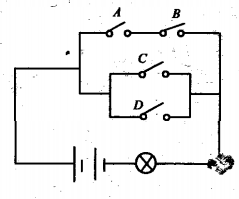
• 1. 如图，在正三棱柱ABC-A₁B₁C₁中，D为BC的中点，AA₁=AB=1.(1)证明：A₁C//平面AB₁D;
  (2)求二面角B-AB₁-D的正切值.
  

• 2. 组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中小张和小赵只能从事前两项工作，其余三人均能从事这四项工作，则不同的选派方案共有多少种?

• 3. 从2,3,4,7,9这五个数字任取3个，组成没有重复数字的三位数，则：(1)这样的三位数一共有多少个?
  (2)所有这些三位数的个位上的数字之和是多少?
  (3)所有这些三位数的和是多少?

• 4. 拟发行体育奖券，号码从000001到999999,购置时揭号兑奖，若规定从个位数起，第一、三、五位是不同的奇数，第二、四、六位均为偶数时为中奖号码，则中奖率约为多少?(精确到0.1%)

• 5. 用2,3,4三个数字排成一个三位数，求排出的数是偶数的概率.