判断题
1、在直角坐标平面内,终边在第一象限的角都是锐角。()
答 案:错
解 析:405°是第一象限的角,但不是锐角
2、正方体不仅相对的面的面积相等,而且所有相邻的面的面积也都相等。()
答 案:对
解 析:正方体有6个面,每个面都是面积相等的正方形,所以,正方体不仅相对的面的面积相等,而且所有相邻的面的面积也都相等
单选题
1、设{an}是公比为正数的等比数列,若a1=1,a5=16,则数列{an}前7项的和为()
- A:63
- B:64
- C:127
- D:128
答 案:C
2、 函数f(x)=ex-2-2的零点所在的区间是()
- A:(0,1)
- B:(1,2)
- C:(2,3)
- D:(3,4)
答 案:C
解 析:计算得到f(2)f(3)<0即得解由题得f(2)f(3)<0即得解。由题得f(2)=e2-2-2=-1<0,f(3)=e3-2-2>0,所以f(2)f(3)<0所以f(2)f(3)<0,所以函数f(x)=ex-2-2的零点所在的区间是(2,3)。故选:C
多选题
1、已知向量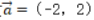 ,
,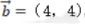 ,则()
,则()
- A:
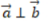
- B:
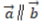
- C:
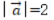
- D:
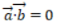
答 案:AD
解 析:若设a=(x1,y1),b=(x2,y2),a⊥b的充要条件是a·b=0,即(x1x2+y1y2)=0。本题中-2*4+2*4=0,则两个向量垂直
2、已知数列{3n-1},下面选项正确的是()
- A:这个数列是公比为3的等比数列
- B:这个数列是公差为3的等差数列
- C:这个数列的第5项是14
- D:20是这个数列的第7项
答 案:BCD
解 析:已知数列{3n-1},这个数列是公差为3的等差数列,故A错误,B正确。数列第五项=3*5-1=14。故C正确。数列第七项=3*7-1=20.故D正确
主观题
1、已知等差数列{an}的前n项和Sn且S5=35,S8=104.
(1)求数列{an}的通项公式;
(2)若{bn}为等比数列,b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
答 案:(1)
 所以a6=19.则数列{an}的公差
所以a6=19.则数列{an}的公差 ,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以
,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以 则
则
2、某投资商计划用60万元投资甲、乙两个项目.根据预判,甲项目最大亏损率为20%,乙项目最大亏损率为30%,最大亏损不能超过16万元;甲、乙两个项目的最大盈利率分别为70%和60%.问投资商对甲、乙两个项目分别投资多少万元时,才能使盈利最大?最大盈利是多少万元?
答 案:设投资商对甲、乙两个项目分别投资x,y万元,获得的盈利为z万元,则有 目标函数z=0.7x+0.6y,
作可行域,如图所示:
目标函数z=0.7x+0.6y,
作可行域,如图所示:
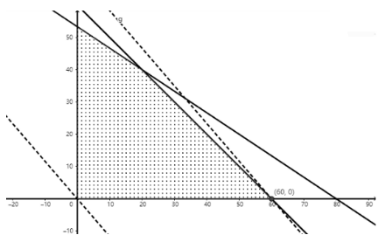 作0等值线l0:0.7x+0.6y=0,并平移0等值线,当直线l0经过可行域中的点(60,0)时,目标函数z取到最大值
所以,当x=60,y=0时,最大盈利为0.7×60+0.6×0=42(万元)
因此,投资商对甲、乙两个项目分别投资60万元和0万元才能使盈利最大,最大盈利为42万元
作0等值线l0:0.7x+0.6y=0,并平移0等值线,当直线l0经过可行域中的点(60,0)时,目标函数z取到最大值
所以,当x=60,y=0时,最大盈利为0.7×60+0.6×0=42(万元)
因此,投资商对甲、乙两个项目分别投资60万元和0万元才能使盈利最大,最大盈利为42万元
填空题
1、经过点A(2,1),与直线2x+y-10=0垂直的直线方程是______
答 案:x-2y=0
2、函数y= log2 (x2-4x+3) 的单调递减区间是______.
答 案:(-∞,1)
解 析:由x2-4x+3>0,得x< 1或x>3.
令g(x)=x2-4x+3 ,其对称轴方程为x= 2.
所以函数g(x)=x2-4x+3在(3, +∞)上为单调递增,在(-∞,1)上单调递减
又函数y= log2 t 为增函数,同增异减
所以函数y = log2(x2 - 4x + 3)的递减区间为(-∞,1).
故答案为(-∞,1).

