判断题
1、甲车间的出勤率比乙车间高，说明甲车间人数比乙车间人数多。()
答 案：错
解 析：出勤率=出勤人数÷全体人数×100%，所以出勤率的高低决定于出勤人数和全体人数的比，例如：甲车间有40人，出勤40人，出勤率为100%；乙车间有50人，出勤48人，出勤率是96%；虽然甲车间出乙车间出勤率高，但人数却少于车间班，所以本题说法错误；故答案为：错误。
2、在统计中，被抽取出来的个体的集合叫做样本容量。（）
答 案：错
解 析：应该是样本。要考察的全体对象叫做总体。组成总体的每一个考察对象叫个体。抽样调查中，被抽取的那些个体叫样本。样本中个体的数目叫样本容量。
单选题
1、如图，在三棱锥P-ABC中，PC⟂平面ABC，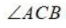
=90°，BC=3，AC=4，PC=1，则点P到直线AB的距离是（） 
- A：16/5
- B：3
- C：14/5
- D：13/5
答 案：D
解 析：
2、直线y=k(x-1)+2与抛物线x2=4y的位置关系为（）
- A：相交
- B：相切
- C：相离
- D：不能确定
答 案：A
多选题
1、已知向量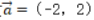
，
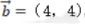，则（）
- A：
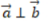
- B：
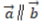
- C：
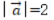
- D：
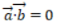
答 案：AD
解 析：若设a=(x1,y1)，b=(x2,y2)，a⊥b的充要条件是a·b=0，即(x1x2+y1y2)=0。本题中-2*4+2*4=0，则两个向量垂直
2、已知数列{3n-1}，下面选项正确的是（）
- A：这个数列是公比为3的等比数列
- B：这个数列是公差为3的等差数列
- C：这个数列的第5项是14
- D：20是这个数列的第7项
答 案：BCD
解 析：已知数列{3n-1}，这个数列是公差为3的等差数列，故A错误，B正确。数列第五项=3*5-1=14。故C正确。数列第七项=3*7-1=20.故D正确
主观题
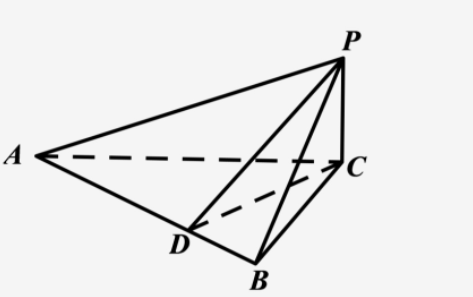
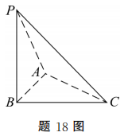
1、如图所示，在三棱锥P-ABC中，PB⊥平面ABC,AB⊥AC,垂足为点A
(1)证明：AC⊥平面PAB;
(2)若AC=3,BC=√10,直线PC与平面PAB所成的角为30°,求三棱锥B-PAC的体积.
答 案：（1）证明：因为PB⊥平面ABC，AC⊆平面ABC，所以PB⊥AC 又因为AB⊥AC，AB,PB⊆平面PAB，AB∩PB=B,
所以AC⊥平面PAB
（2）因为直线PC与平面PAB所成的角为30°，AC⊥平面PAB，
所以在直角三角形PAC中，∠CPA=30°,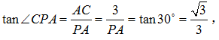
解得PA=3√3
又因为△ABC的面积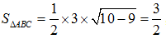
，PB⊥平面ABC
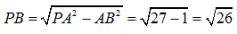所以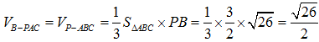
2、已知函数f(x)=log3(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.
答 案：(1)根据题意可得，3x-1>0,解得
所以函数f(x)的定义域是
(2)因为f(x)=log3(3x-1)<1=log33,f(x)为定义域上的增函数，所以O<3x-1<3,解得
所以x的取值范围是
填空题
1、过点（-1，2）且在两坐标轴上截距相等的直线方程为______．
答 案：2x+y=0或x+y-1=0
解 析：当直线过原点时，直线的斜率k=-2，直线方程为y=-2x，即2x+y=0；当直线不过原点时，设直线方程为x+y=a，代入点（-1，2）得：-1+2=a，即a=1。∴直线方程为：x+y-1=0。∴过点（-1，2）且在两坐标轴上截距相等的直线方程为2x+y=0或x+y-1=0
2、“x∈A∩B”是“x∈AUB”的（）条件。
答 案：充分不必要
解 析：可通过画集合的Venn图得到“x∈A∩B”是“x∈AUB”的充分不必要条件.
