单选题

1、在等比数列{a_n}中，a₂=9,a₅=243,则{a_n}的前4项和为()  

• A：81
• B：120
• C：168
• D：192

答 案：B

解 析：设等比数列{a}的公比为q.由题意得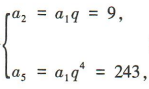解得a₁=3,q=3,故a₃=a₂q=27,a₄=a₃q=81,所以{a,}的前4项和S₄=a₁+a₂+a₃+a₄=3+9+27+81=120.

2、椭圆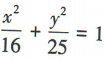的两个焦点分别为F₁,F₂,过F₂的直线交椭圆于A,B两点，则△ABF₁的周长是()  

• A：10
• B：12
• C：16
• D：20

答 案：D

解 析：由题意得椭圆的长半轴长a=5.由椭圆定义可知，|AF₁|+|AF₂|=|BF₁|+|BF₂|=2a=10,所以△ABF₁的周长为|AF₁|+|AB|+|BF₁|=|AF₁|+|AF₂|+|BF₂|+|BF₁|=20.

3、已知命题p:x∈(A∪B),则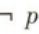是（）

• A：x∉(A∩B)
• B：x∉A或x∉B
• C：x∉A且x∉B
• D：x∈(A∩B)

答 案：C

解 析：由x∈(A∪B)知x∈A或x∈B,所以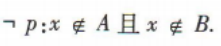

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、直线y=x-1被圆C:x²+y²-4x=0所截得的弦长为（）  

答 案：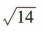

解 析：由x²+y²-4x=0得(x- 2)²+y²=4,所以圆C的圆心为(2,0),半径r=2,所以圆心C到直线y=x-1的距离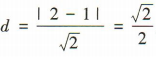,所以所求弦长为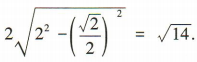

2、函数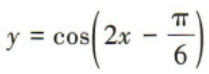的最小正周期为（）

答 案：π

解 析：

3、不等式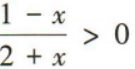的解集为（）

答 案：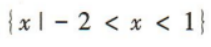

解 析：

简答题

1、已知椭圆的中心为原点，焦点在x轴上，离心率为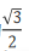，且经过点M(4，1)，直线l：y=x+m交椭圆于异于M的 不同两点A、B,直线MA、MB与x轴分别交于点E、F. (1)求椭圆的标准方程；(2)求m的取值范围  

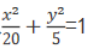答 案： (2)将y=x+m代入并整理，得5x2+8mx+4m2-20=0 令△=(8m)2-20(4m2-20)＞0,解得-5＜m＜5. 又，由题意可知，直线不过M(4，1)， 所以4+m≠1，m≠-3, 所以m的取值范围是(-5,-3)∪(-3,5).