2025年成考专升本《高等数学一》每日一练试题06月17日
精选习题
2025-06-17
11:30:31
收藏
单选题
1、设f(x)为连续函数,则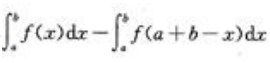 等于()。
等于()。
- A:0
- B:1
- C:a+b
- D:
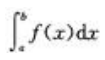
答 案:A
解 析:对于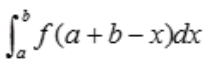 ,令
,令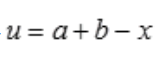 ,则
,则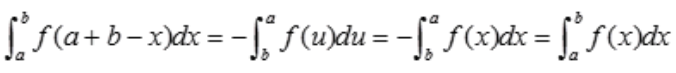 故原式=
故原式=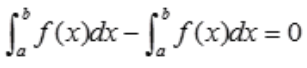 。
。
2、设z=2x2+3xy-y2,则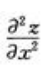 等于()。
等于()。
- A:4
- B:3
- C:2
- D:-2
答 案:A
解 析: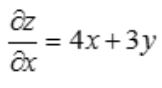 ,
,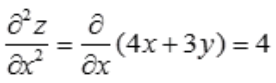 。
。
3、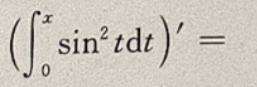
- A:sin2x
- B:sin2x
- C:cos2x
- D:-sin2x
答 案:B
解 析:由变上限定积分的定理可知
主观题
1、设z=f(x,y)是由方程 所确定,求
所确定,求 。
。
答 案:解:由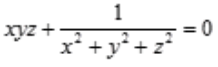 得全微分方程:
得全微分方程: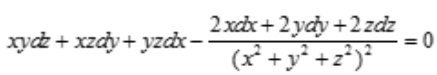 化简得
化简得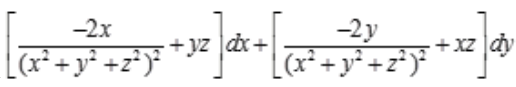
 所以
所以
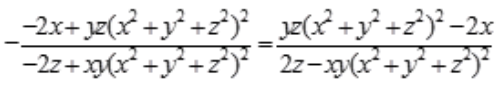 。
。
2、将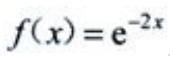 展开为x的幂级数。
展开为x的幂级数。
答 案:解:因为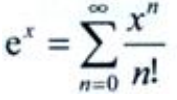 ,
, ,所以
,所以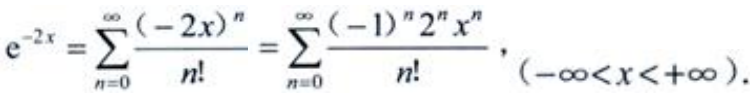
3、求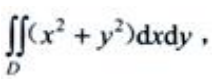 其中
其中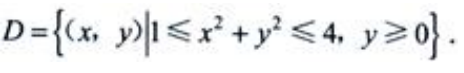
答 案:解:D在极坐标系下可以表示为 则
则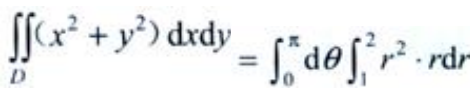
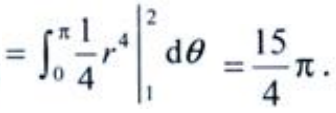
填空题
1、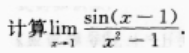
答 案:
解 析: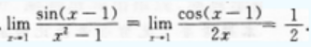
2、设曲线y=f(x)在点(1,f(1))处的切线平行于x轴,则该切线方程()。
答 案:y=f(1)。
解 析:本题考查的知识点有两个:一是导数的几何意义,二是求切线方程。设切点为(x0,f(x0)),则曲线y=f(x)过该点的切线方程为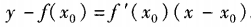


3、设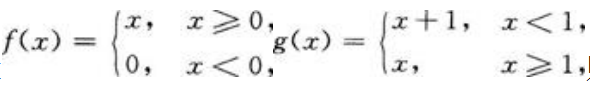 则F(x)=f(x)+g(x)的间断点是()。
则F(x)=f(x)+g(x)的间断点是()。
答 案:x=1
解 析:由于f(x)有分段点x=0,g(x)有分段点x=1,故需分三个区间讨论F(x)=f(x)+g(x)的表达式,而x=0,x=1的函数值单独列出,整理后得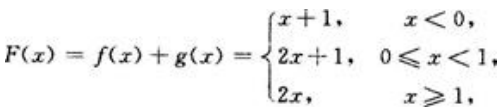 又因
又因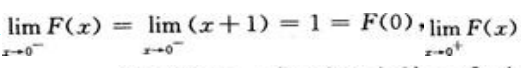
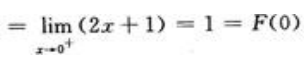 所以x=0是F(x)的连续点,而
所以x=0是F(x)的连续点,而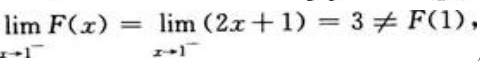 所以x=1是F(x)的间断点。
所以x=1是F(x)的间断点。
简答题
1、求微分方程y”-y’-2y=3ex的通解。
答 案:

解 析:本题考查的知识点为求解二阶线性常系数非齐次微分方程。 
更多推荐

