判断题

1、已知函数f（x）的定义域为[-1，5]、在同一坐标系下，函数y=f（x）的图象与直线x=1的交点个数为（　　）  

答 案：对

解 析：∵f（x）的定义域为[-1，5]，而1∈[-1，5]，∴点（1，f（1））在函数y=f（x）的图象上。而点（1，f（1））又在直线x=1上，∴直线x=1与函数y=f（x）的图象至少有一个交点（1，f（1））。根据函数的定义知，函数是一个特殊的映射，即对于定义域[-1，5]中的任何一个元素，在其值域中只有唯一确定的元素f（1）与之对应，故直线x=1与y=f（x）的图象有且只有一个交点。

2、点(-1,-3)关于y轴的对称点为(-1,3)。（）  

答 案：错

解 析：关于y轴的对称点的坐标特征是横坐标相反，纵坐标相同，所以点(-1,-3)关于y轴的对称点为(1,-3)

单选题

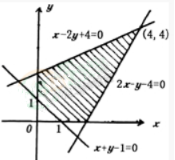
1、已知动点(x，y)所在的区域是如图所示的阴影部分(包括边界)，则目标函数z=x+2y的最小值和最大值分别()  

• A：2,12
• B：2,4
• C：1,12
• D：1,4

答 案：C

解 析：先根据可行域中的五个角点：（1，0），（0，1），（0，2），（4，4），（2，0）。z=x+2y过点（4，4）时，z最大是12，z=x+2y过点（1，0）时，z最小是1，故选C。

2、双曲线的两条渐近线互相垂直，则双曲线的离心率为（）  

• A：
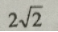
• B：
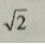
• C：
• D：

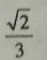
答 案：B

多选题

1、已知等差数列{a_n}的前n项和为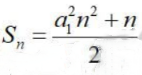，公差为d，则（）  

• A：a₁=1
• B：d=1
• C：
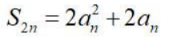
• D：2S_n-a_n=1+3+5+...+(2n-1)

答 案：ABD

2、下列四个命题中正确的是（）  

• A：与圆有公共点的直线是该圆的切线
• B：垂直于圆的半径的直线是该圆的切线
• C：到圆心的距离等于半径的直线是该圆的切线
• D：过圆直径的端点，垂直于此直径的直线是该圆的切线

答 案：CD

解 析：A中，与圆有两个公共点的直线，是圆的割线，故该选项不符合题意；B中，应经过此半径的外端，故该选项不符合题意；C中，根据切线的判定方法，故该选项符合题意；D中，根据切线的判定方法，故该选项符合题意。故选：CD。

主观题

1、在等差数列{a_n}中，a₅=-10,a₁₀=0. (1)求数列{a_n}的通项公式； (2)记数列{a_n}的前n项和为S_n,当n为何值时，S_n有最小值?最小值是多少?  

答 案：（1）设等差数列{a_n}的公差为d， 则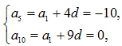解得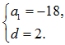 因此，数列{a_n}的通项公式为a_n=-18+2(n-1)，即a_n=2n-20 （2）由等差数列的前n项和公式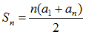得 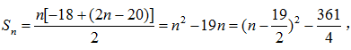所以当n=9或n=10时，S_n有最小值-90  

2、如图所示，在平面四边形ABCD中，AB=√5,AC=3,BC=2√2. 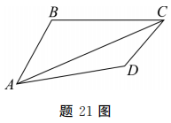(1)求∠ACB的大小； (2)若cos∠ADC=,cos∠BCD=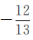,求线段AD的长.  

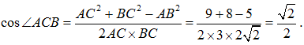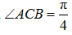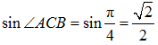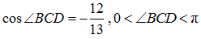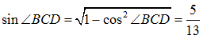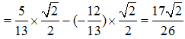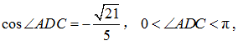答 案：（1）在△ABC中，由余弦定理得 因为0＜∠ACB＜π，所以 （2）由（1）可知 因为，所以 Sin∠ACD=sin(∠BCD-∠ACB)=sin∠BCDcos∠ACB-cos∠BCDsin∠ACB 又因为 所以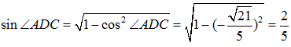 在△ACD中，由正弦定理得 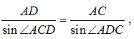所以  

填空题

1、若（x-1）²=2，则代数式x²-2x+5的值为多少（）  

答 案：6

2、平面上A（-2，1），B（1，4），D（4，-3），C点满足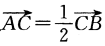，连接DC并延长至E，使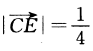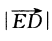，则点E坐标为________  

答 案：