判断题
1、在同一平面内，过一点有且只有一条直线与已知直线垂直。（）
答 案：对
解 析：根据垂线的性质:平面内,过一点有且只有一条直线与已知直线垂直
2、函数y=（1/2）x在（-∞，+∞）单调增加。（）
答 案：错
单选题
1、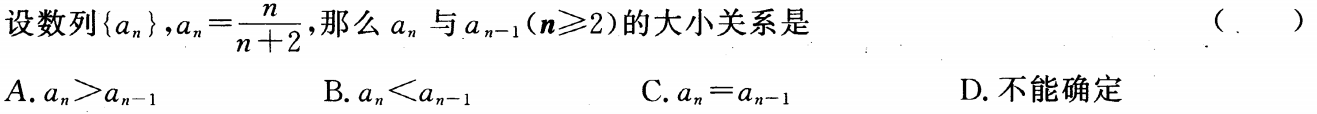
- A：A
- B：B
- C：C
- D：D
答 案：A
2、函数
的图像大致是（）
- A：
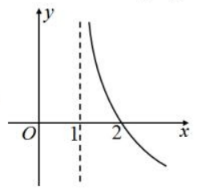
- B：
- C：
- D：
答 案：A
多选题
1、下列命题中，不正确的是（）
- A：三点可确定一个圆
- B：三角形的外心是三角形三边中线的交点
- C：一个三角形有且只有一个外接圆
- D：三角形的外心必在三角形的内部或外部
答 案：ABD
解 析：A、不在同一条直线上的三点确定一个圆，故本选项错误；B.、三角形的外心是三角形三边垂直平分线的交点，所以本选项是错误；C、三角形的外接圆是三条垂直平分线的交点，有且只有一个交点，所以任意三角形一定有一个外接圆，并且只有一个外接圆，所以本选项是正确的；D、直角三角形的外心在斜边中点处，故本选项错误。故选：ABD
2、下列四个命题中正确的是（）
- A：与圆有公共点的直线是该圆的切线
- B：垂直于圆的半径的直线是该圆的切线
- C：到圆心的距离等于半径的直线是该圆的切线
- D：过圆直径的端点，垂直于此直径的直线是该圆的切线
答 案：CD
解 析：A中，与圆有两个公共点的直线，是圆的割线，故该选项不符合题意；B中，应经过此半径的外端，故该选项不符合题意；C中，根据切线的判定方法，故该选项符合题意；D中，根据切线的判定方法，故该选项符合题意。故选：CD。
主观题
1、已知抛物线C:x2=4y和直线7:2x+2y+m=0. (1)若抛物线C和直线l有两个交点，求m的取值范围； (2)若m＞1,且直线l与抛物线C有两个交点A,B,线段AB的垂直平分线交y轴于点P,求△PAB的面积S的取值范围。
答 案：（1）由2x+2y+m=0得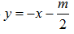
将其代入x2=4y中得x2+4x+2m=0，
所以△=42-4×1×2m=16-8m.
因为抛物线C和直线l有两个交点，所以△=16-8m＞0，解得m＜2.
因此，m的取值范围是（-∞，2）
（2）设点A（x1，,y1），B（x2，y2），则由方程x2+4x+2m=0可得x1+x2=-4，x1x2=2m，
（x1-x2)2=（x1+x2)2-4x1x2=8（2-m）;
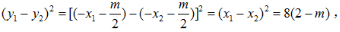所以
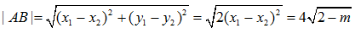因为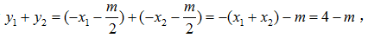
所以线段AB的中点
kAB=-1，
所以过点Q与线段AB垂直的直线方程为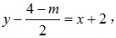
即2x-2y+8-m=0.
该直线与y轴的交点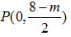
到直线l的距离
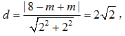所以△PAB的面积
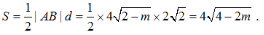因为1＜m＜2，所以0＜4-2m＜2，
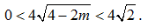因此，△PAB的面积S的取值范围是（0，4√2）
2、在等差数列{an}中，a5=-10,a10=0. (1)求数列{an}的通项公式； (2)记数列{an}的前n项和为Sn,当n为何值时，Sn有最小值?最小值是多少?
答 案：（1）设等差数列{an}的公差为d， 则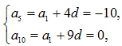
解得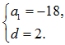
因此，数列{an}的通项公式为an=-18+2(n-1)，即an=2n-20
（2）由等差数列的前n项和公式
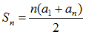得
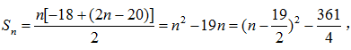所以当n=9或n=10时，Sn有最小值-90
填空题
1、在下列六个图形中，每个小四边形皆为全等的正方形，那么沿其正方形相邻边折叠，能够围成正方体的是______（把你认为正确的图形序号都填上）.
答 案：(1)(3)(6）
2、比较m，n的大小：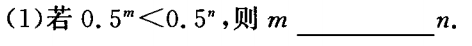 
答 案：（1）>（2）<
解 析：考察指数函数的单调性
底数 0.5∈（0,1）单调递减，m＞n
底数 3∈（1，+∞）单调递增，m＜n
