单选题

1、若椭圆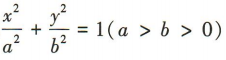的焦距为2,离心率为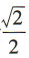,则椭圆的方程为()  

• A：
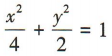
• B：
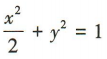
• C：
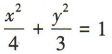
• D：

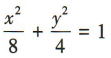
答 案：B

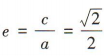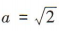解 析：由题意可知 2c = 2,即c=1.由椭圆的离心率得,所以b²=α²-c²=1,所以椭圆的标准方程为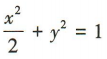

2、一个盒子中有20张奖券,其中一等奖2张,二等奖4张,三等奖8张,小明从盒子中任取一张奖券,小明中奖的概率是（）  

• A：
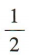
• B：
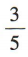
• C：
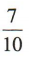
• D：

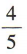
答 案：C

解 析：20张奖券中,中奖奖券共有2+4+8=14(张),所以小明中奖的概率是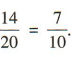

3、抛物线y²=16x的焦点到准线的距离是()

• A：8
• B：4
• C：
• D：

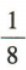
答 案：A

解 析：因为抛物线的标准方程为y²=16x,所以2p=16,即p=8,所以抛物线y²=16x的焦点到准线的距离是8.

主观题

1、已知

答 案：方法一：矢量图表示法 矢量图表示法如图所示。 方法二：矢量表示法

解 析：

填空题

1、若向量a=(-2,1),b=(1,3),c=a+2b,则c=（）

答 案：（0,7）

解 析：由a=(-2,1),b=(1,3),得c=a+2b=(0,7).

2、已知以 F₁,F₂为焦点的椭圆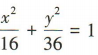交x轴正半轴于点4,则△AF₁F₂的面积为()  

答 案：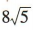

解 析：由题意得a²= 36,b²= 16,所以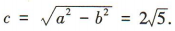因为椭圆与x轴正半轴交于点A,所以A(4,0),所以

3、过直线2x-y+4=0与x-y+5=0的交点,且垂直于直线x-2y=0的直线的方程为（）  

答 案：2x+y-8=0

解 析：由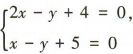得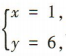所以直线2x-y+4=0与x-y+5=0的交点为(1,6).因为垂直于直线x-2y=0的直线的斜率为-2,所以所求直线的方程为y-6=-2(x-1),即2x+y-8=0.

简答题

1、如图所示，动物园要建造一面靠墙的2间面积相同的矩形熊猫居室，已知可供建造围墙的材料总长是36m (1)把2间熊猫居室的总面积S(单位：m²)表示为宽x(单位：m)的函数，求该函数的解析式，并写出定义域 (2)当宽为多少时，才能使所建造的每间熊猫居室面积最大?每间熊猫居室最大面积是多少?

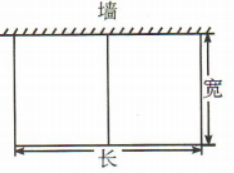
答 案：(1)由题意得矩形的长为36-3x,