2025年高职单招《数学(中职)》每日一练试题06月02日
精选习题
2025-06-02
16:02:32
收藏
单选题
1、已知tanα=2,则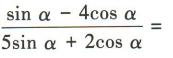 ()
()
- A:
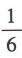
- B:
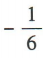
- C:6
- D:-6
答 案:B
解 析:因为tanα=2,所以
2、在等比数列{an}中,a1=2,a4=54,则公比q=()
- A:2
- B:3
- C:4
- D:5
答 案:B
解 析:∵数列{an}为等比数列,∴a4=a1q³.又a1=2,a4=54,∴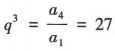 ,∴q=3.
,∴q=3.
3、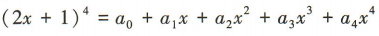 ,则
,则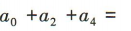
- A:41
- B:40
- C:-40
- D:-41
答 案:A
解 析:令x=1,得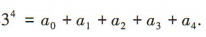 令x=-1,得
令x=-1,得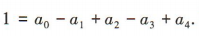 两式相加得
两式相加得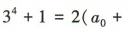
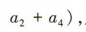 所以
所以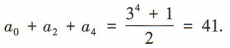
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、已知函数f(x)=2x-m在[0,2]上的最小值为2,则f(m)=()
答 案:
解 析: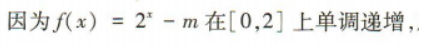
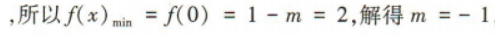
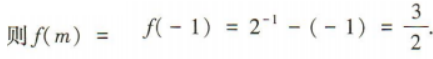
2、从一个12男11女的班级中任选一人进行问卷调査,抽到的是女同学的概率为()
答 案: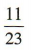
解 析:因为班级的人数为 12+11= 23,所以抽到的是女同学的概率为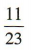
3、设等差数列{an}的前n项和为Sn,若Sm-1,=-2,Sm=0,Sm+1=3,则公差d=()
答 案:1
解 析:因为Sm-1=-2,Sm=0,Sm+1=3,所以am=Sm-Sm-1=2,am+1=Sm+1-Sm=3,所d=am+1-am=1.
简答题
1、某商场出售两款型号不同的手机,由于市场需求发生变化,第一款手机连续两次提价10%,第二款手机连续两次降价10%,结果都以1 210元出售 (1)求第一款手机的原价; (2)若该商场同时出售两款手机各一部,求总售价与总原价之间的差额.(结果保留整数)
答 案: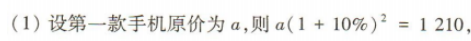
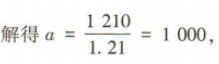

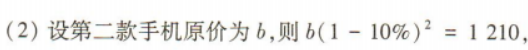
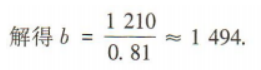

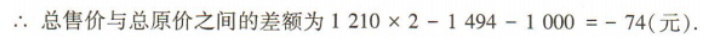
更多推荐

