2025年高职单招《数学(中职)》每日一练试题05月28日
精选习题
2025-05-28
15:50:16
收藏
单选题
1、在等差数列{an}中,a1=-3,公差d=3,若此数列前n项的和Sn=27,则n=()
- A:5
- B:6
- C:7
- D:8
答 案:B
解 析:在等差数列{a}中,a1=-3,d=3,所以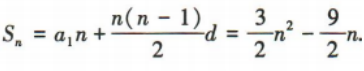 因为Sn=27,所以
因为Sn=27,所以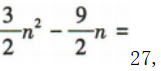 即n²-3n-18=0,解得n=6或n=-3(舍).
即n²-3n-18=0,解得n=6或n=-3(舍).
2、若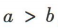 ,则下列结论正确的是()
,则下列结论正确的是()
- A:
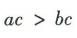
- B:
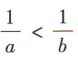
- C:

- D:

答 案:D
解 析:当c=0时,ac=bc,故A错误;当a=1,b=-2时,满足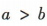 ,且
,且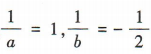 ,a²=1,b²=4,此时
,a²=1,b²=4,此时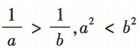 ,故B,C错误;不等式
,故B,C错误;不等式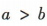 两边同时加上同一个数c,不等号的方向不变,所以
两边同时加上同一个数c,不等号的方向不变,所以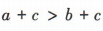 ,故D正确
,故D正确
3、下列函数中,定义域为(0,+∞)的是()
- A:f(x)=ex
- B:f(x)=Inx
- C:

- D:f(x)=|x|
答 案:B
解 析:函数f(x)=ex的定义域为R,故A不符合题意;函数f(x)=Inx的定义域为(0,+∞),故B符合题意;函数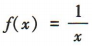 的定义域为{xlx≠0},故C不符合题意;函数f(x)=|x|的定义域为R,故D不符合题意.
的定义域为{xlx≠0},故C不符合题意;函数f(x)=|x|的定义域为R,故D不符合题意.
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、已知函数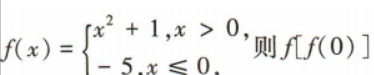 的值为()
的值为()
答 案:-5
解 析:由题意得f(0)=-5,所以f[f(0)]=f(-5)=-5.
2、已知函数f(x)=x2-2ax+3的值域是[-1,+∞),则a=()
答 案:±2
解 析:易得f(x)=x2-2ax+3=(x-a)2-a2+3,故f(x)min=f(a)=-a2+3=-1,解得a=2或a=-2.
3、某校有 900名学生,其中女生 400名.按男女比例用分层抽样的方法,从该校学生中抽取一个容量为45 的样本,则应抽取男生的人数为()
答 案:25
解 析:应抽取男生的人数为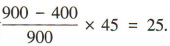
简答题
1、已知在等差数列{an}中,a3=5,a17=3a6
(1)求数列{an}的通项公式;
(2)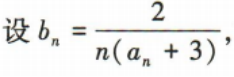 求数列{bn}的前100项和S100
求数列{bn}的前100项和S100
答 案: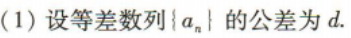

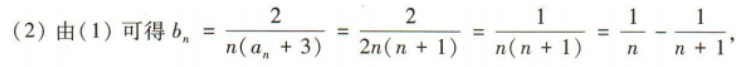
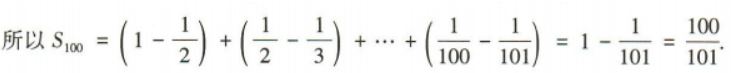
更多推荐

