2025年高职单招《数学(中职)》每日一练试题05月24日
精选习题
2025-05-24
15:42:01
收藏
单选题
1、若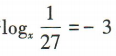 ,则x=()
,则x=()
- A:81
- B:
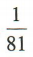
- C:
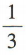
- D:3
答 案:D
解 析:因为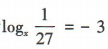 ,所以
,所以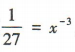 ,即x³=27,所以x=3.
,即x³=27,所以x=3.
2、下列函数中,在R上为增函数的是()
- A:f(x)=-x
- B:f(x)=x²
- C:f(x)=2x
- D:f(x)=cos x
答 案:C
解 析:易得f(x)=-x在R上为减函数,故A不符合题意.易知f(x)=x2在(-∞,0)上单调递减,在(0,+∞)上单调递增,故B不符合题意.由指数函数的性质知,f(x)=2x在R上为增函数,故C符合题意;由余弦函数的性质知f(x)=cosx在R上不单调,故D不符合题意.
3、函数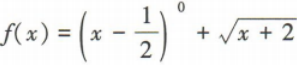 的定义域为()
的定义域为()
- A:
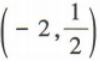
- B:[-2,+∞)
- C:
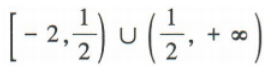
- D:
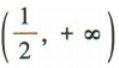
答 案:C
解 析:要使函数f(x)有意义,须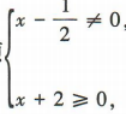 解得
解得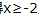 且
且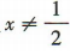 ,所以f(x)的定义域为
,所以f(x)的定义域为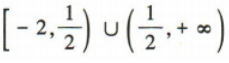
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、已知tanα=2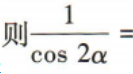 ()
()
答 案: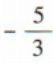
解 析: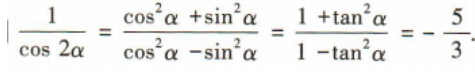
2、关于x的不等式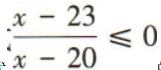 的解集是()
的解集是()
答 案:(20,23]
解 析: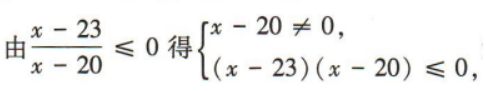
 (20,23]
(20,23]
3、若 则cos(π-α)=()
则cos(π-α)=()
答 案:
解 析:
简答题
1、已知双曲线C的中心在原点,焦点在x轴上,焦距为 10,一条渐近线方程为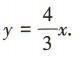 (1)求C的标准方程;(2)过C的右顶点,且斜率为2的直线l交C于A,B两点,求|AB|.
(1)求C的标准方程;(2)过C的右顶点,且斜率为2的直线l交C于A,B两点,求|AB|.
答 案:(1)依题意可设C的标准方程为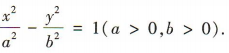 ∵双曲线的焦距为 10,
∴c=5.
∵C的一条渐近线方程为
∵双曲线的焦距为 10,
∴c=5.
∵C的一条渐近线方程为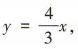 ∴
∴ 又a2+b2=c2,
∴a=3,b=4.
∴C的标准方程为
又a2+b2=c2,
∴a=3,b=4.
∴C的标准方程为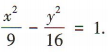 (2)由(1)得C的右顶点为(3,0).
∵直线l的斜率为2,且过C的右顶点,
∴直线l的方程为y=2x-6.
由
(2)由(1)得C的右顶点为(3,0).
∵直线l的斜率为2,且过C的右顶点,
∴直线l的方程为y=2x-6.
由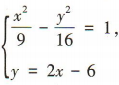 得5x2-54x+117=0,解得
得5x2-54x+117=0,解得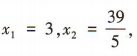 ∴
∴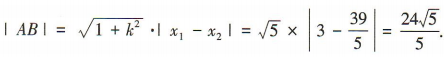
更多推荐

