2025年成考专升本《高等数学一》每日一练试题05月22日
精选习题
2025-05-22
11:34:27
收藏
单选题
1、设函数f(x)在(0,1)上可导且在[0,1]上连续,且f'(x)>0,f(0)<0,f(1)>0,则f(x)在(0,1)内()。
- A:至少有一个零点
- B:有且仅有一个零点
- C:没有零点
- D:零点的个数不能确定
答 案:B
解 析:因为函数f(x)在[0,1]上连续,f(0)<0,f(1)>0,故存在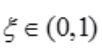 ,使得
,使得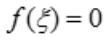 ,又f'(x)>0,函数在(0,1)上单调增加,故f(x)在(0,1)内有且仅有一个零点。
,又f'(x)>0,函数在(0,1)上单调增加,故f(x)在(0,1)内有且仅有一个零点。
2、下列函数在[1,e]上满足拉格朗日中值定理条件的是()。
- A:1/(1-x)
- B:lnx
- C:1/(1-lnx)
- D:
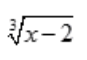
答 案:B
解 析:AC两项,在[1,e]不连续,在端点处存在间断点(无穷间断点);B项,lnx在[1,e]上有定义,所以在[1,e]上连续,且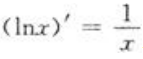 在(1,e)内有意义,所以lnx在(1,e)内可导;D项,定义域为[2,+∞],在[1,2)上无意义。
在(1,e)内有意义,所以lnx在(1,e)内可导;D项,定义域为[2,+∞],在[1,2)上无意义。
3、设y= ,则dy=()。
,则dy=()。
- A:
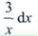
- B:

- C:

- D:
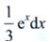
答 案:A
解 析: 。
。
主观题
1、判断级数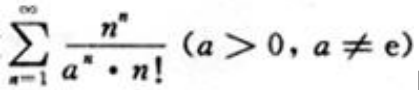 的敛散性。
的敛散性。
答 案:解:令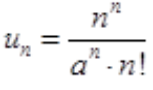 ,则
,则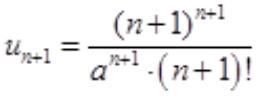 ,由于
,由于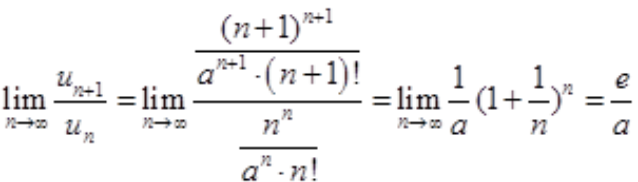 故有当
故有当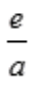 <1,即a>e时,该级数收敛;当
<1,即a>e时,该级数收敛;当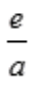 >1,即a<e时,该级数发散。
>1,即a<e时,该级数发散。
2、求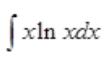 。
。
答 案:解: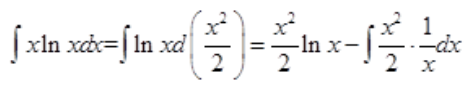
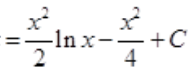 。
。
3、求微分方程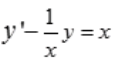 的通解。
的通解。
答 案:解: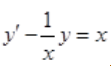 为一阶线性微分方程,则
为一阶线性微分方程,则
填空题
1、函数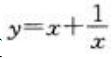 的极大值点的坐标是()。
的极大值点的坐标是()。
答 案:(-1,-2)
解 析: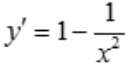 ,令y'=0,得
,令y'=0,得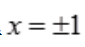 .当x<-1时,y'>0,函数单调增加;当
.当x<-1时,y'>0,函数单调增加;当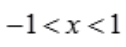 时,y'<0,函数单调减少;当x>1时,y'>0,函数单调增加.故当x=-1时,函数取得极大值为-2,即极大值坐标为(-1,-2)。
时,y'<0,函数单调减少;当x>1时,y'>0,函数单调增加.故当x=-1时,函数取得极大值为-2,即极大值坐标为(-1,-2)。
2、微分方程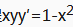 的通解是_____。
的通解是_____。
答 案: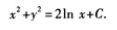
解 析: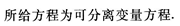

3、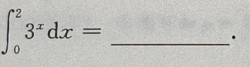
答 案: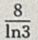
解 析: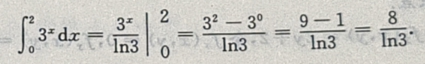
简答题
1、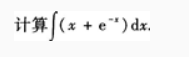
答 案: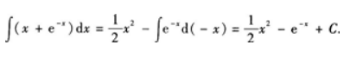
更多推荐

