2025年成考专升本《高等数学一》每日一练试题05月21日
精选习题
2025-05-21
11:39:21
收藏
单选题
1、设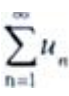 与
与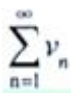 都为正项级数,且
都为正项级数,且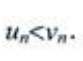 则下列结论正确的是()。
则下列结论正确的是()。
- A:若
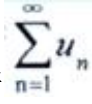 收敛,则
收敛,则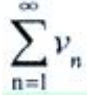 收敛
收敛 - B:若
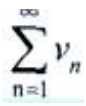 发散,则
发散,则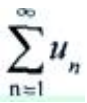 发散
发散 - C:若
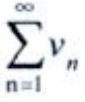 收敛,则
收敛,则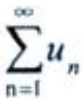 收敛
收敛 - D:若
 收敛,则
收敛,则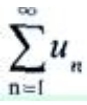 发散
发散
答 案:C
解 析:由正项级数的比较判别法可知,若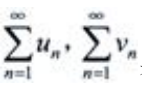 都为正项级数,且
都为正项级数,且 则当
则当 收敛时,可得知
收敛时,可得知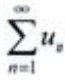 必定收敛.
必定收敛.
2、设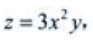 则
则 ()。
()。
- A:6dx+6dy
- B:3dx+6dy
- C:6dx+3dy
- D:3dx+3dy
答 案:C
解 析: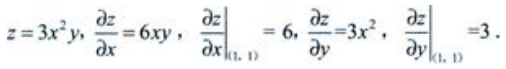
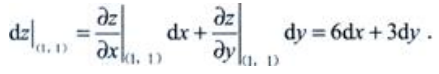
3、∫cos(x-1)dx=()。
- A:sin(x-1)+C
- B:-sin(x-1)+C
- C:sinx+C
- D:-sinx+C
答 案:A
解 析:本题考査的知识点为不定积分运算。 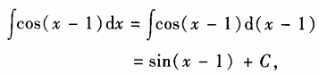 可知应选A。
可知应选A。
主观题
1、设y=(sinx)ex+2,求y'。
答 案:解: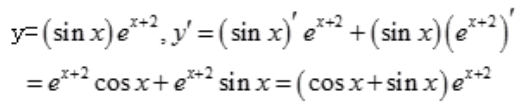
2、求 。
。
答 案:解:
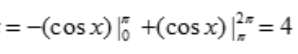 。
。
3、将函数f(x)=sinx展开为 的幂级数.
的幂级数.
答 案:解:由于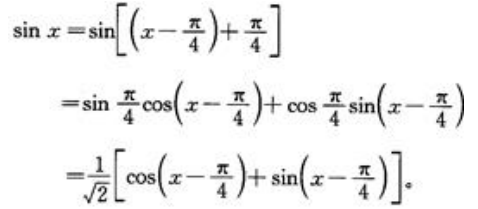 若将
若将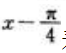 看成整体作为一个新变量,则套用正、余弦函数的展开式可得
看成整体作为一个新变量,则套用正、余弦函数的展开式可得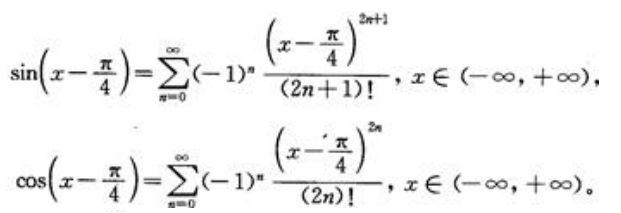 从而有
从而有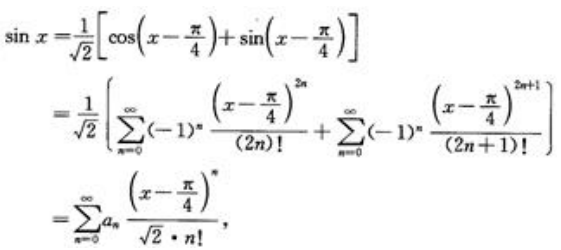 其中
其中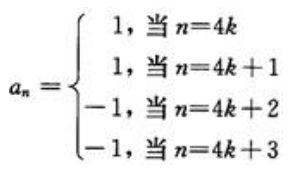 (k为非负整数)。
(k为非负整数)。
填空题
1、设z=ln(x2+y),则dz=()。
答 案: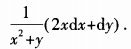
解 析:本题考查的知识点为求二元函数的全微分。 
2、级数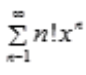 的收敛半径是()。
的收敛半径是()。
答 案:
解 析:
3、设z=sin(y+x2),则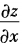 =()。
=()。
答 案:2xcos(y+x2)。
解 析:本题考查的知识点为二元函数的偏导数计算。 
简答题
1、
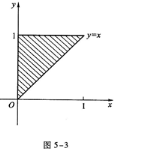
答 案: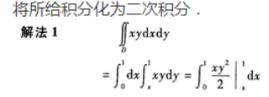
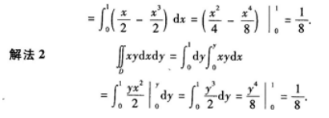
更多推荐

