单选题

1、微分方程y'＋y＝0的通解为y＝（）。

• A：e^-x＋C
• B：－e^-x＋C
• C：Ce^-x
• D：Ce^x

答 案：C

解 析：所给方程为可分离变量方程，分离变量得。两端分别积分。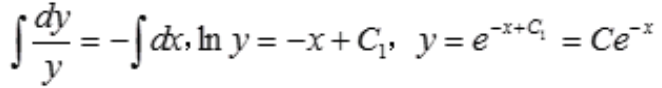

2、函数z＝f(x,y)在点P(x,y)处的偏导数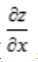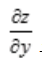，为连续函数，是函数z＝f(x,y)在点P(x,y)处可微分的（）。

• A：充分条件
• B：必要条件
• C：充分必要条件
• D：既非充分也非必要条件

答 案：A

解 析：由多元函数微分的充分条件可知，函数z＝f(x,y)在点P(x,y)处的偏导数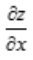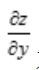，为连续函数，是函数z＝f(x,y)在点P(x,y)处可微分的充分条件。

3、若y＝a^x（a＞0且a≠1），则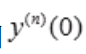等于（）。

• A：lnⁿa
• B：a^xlnⁿa
• C：
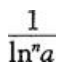
• D：

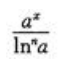
答 案：A

解 析：因为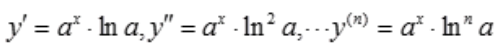，故。

主观题

1、求微分方程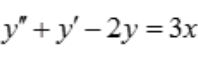的通解。

答 案：解：微分方程的特征方程为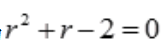，解得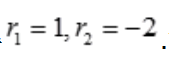.故齐次微分方程的通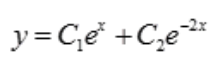解为特解为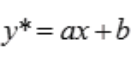，代入微分方程得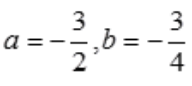。故微分方程的通解为。

2、将函数f（x）＝sinx展开为的幂级数．

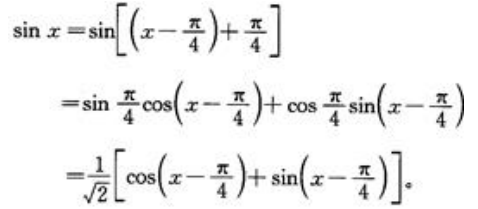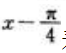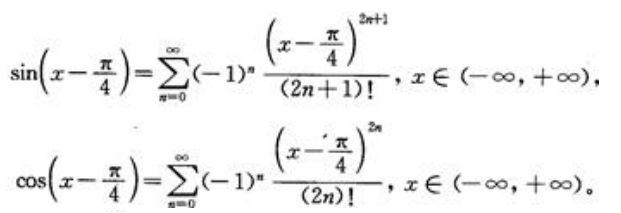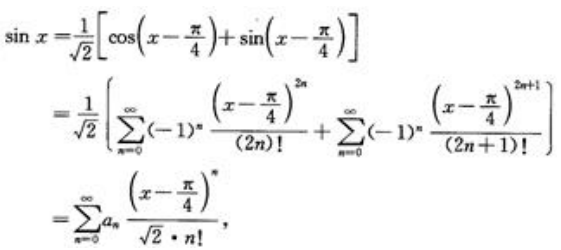答 案：解：由于若将看成整体作为一个新变量，则套用正、余弦函数的展开式可得从而有其中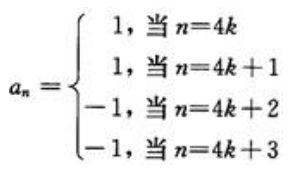（k为非负整数）。

3、设D是由直线y＝x与曲线y＝x³在第一象限所围成的图形.（1）求D的面积S；
（2）求D绕x轴旋转一周所得旋转体的体积V。

答 案：解：由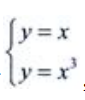，知两曲线的交点为（0，0），（1，1）和（-1，-1），则（1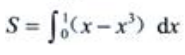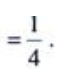）（2）

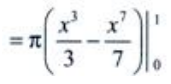
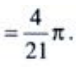
填空题

1、（）。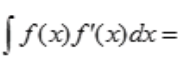

答 案：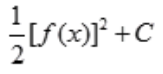

解 析：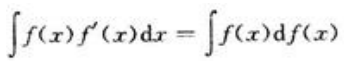

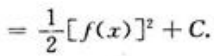
2、过点M₀（1，-1，0）且与平面x-y+3z=1平行的平面方程为＝（）。

答 案：x－y＋3z＝2

解 析：已知平面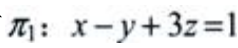的法向量n₁＝（1，－1，3），所求平面π与π₁平行，则平面π的法向量n//n₁，取n＝（1，－1，3），所求平面过点M₀＝（1，－1，0），由平面的点法式方程可知所求平面方程为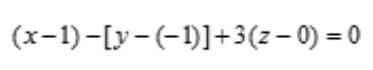，即x－y＋3z＝2。

3、极限＝（）。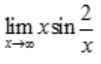

答 案：2

解 析：。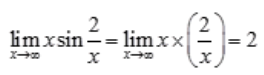

简答题

1、求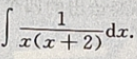  

答 案：