单选题

1、设f（x）在[a，b]上连续，x∈[a，b]，则下列等式成立的是（）。  

• A：
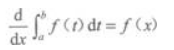
• B：
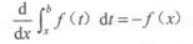
• C：
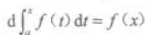
• D：

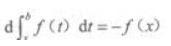
答 案：B

解 析：由可变限积分求导公式知选B。

2、下列方程中表示椭球面的是（）。

• A：x²＋y²－z²＝1
• B：x²－y²＝0
• C：
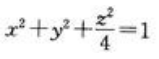
• D：x²＋y²＝z²

答 案：C

解 析：A项，双曲面的方程为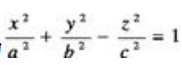，所以为双曲面；B项，x²－y²＝0表示两条垂直的直线；C项，椭球面的方程为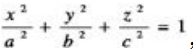，符合这一特征；D项，x²＋y²＝z²表示圆锥体。

3、（）。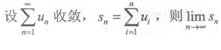  

• A：必定存在且值为0
• B：必定存在且值可能为0
• C：必定存在且值一定不为0
• D：可能不存在 

答 案：B

解 析：由级数收敛的定义可知应选B。

主观题

1、若，求a与b的值。

答 案：解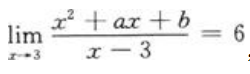：，又x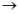3，分母x-3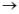0；所以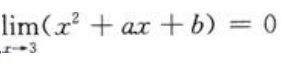，得9＋3a＋b＝0，b＝－9－3a，则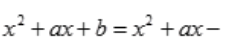（9＋3a）＝（x－3）[x＋（3＋a）]，故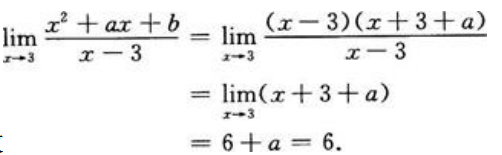a＝0，b＝－9。

2、求过原点且与直线平行的直线的方程．

答 案：解：直线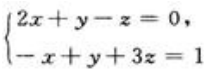的方向向量为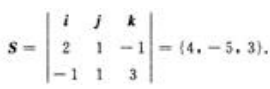因所求直线与已知直线平行，所以所求直线的方向向量也为s．所求直线过原点．故由标准式可得所求直线的方程为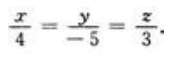

3、在曲线上求一点M₀，使得如图中阴影部分的面积S₁与S₂之和S最小。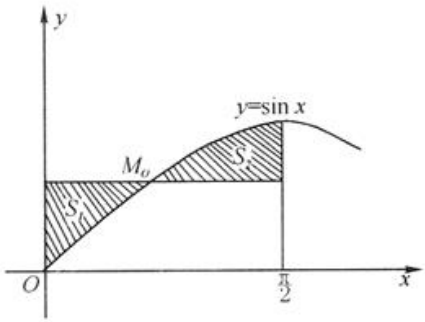

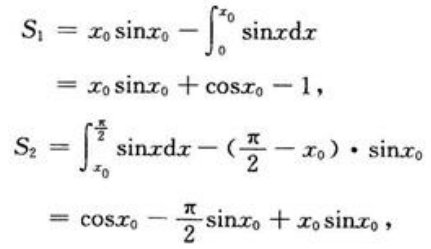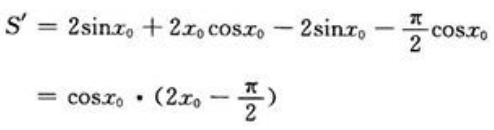答 案：解：设点M₀的横坐标为x₀，则有则S为x₀的函数，将上式对x₀求导得令S'=0,得，所以由于只有唯一的驻点，所以则点M₀的坐标为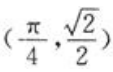为所求。

填空题

1、设，则（）

答 案：0

解 析：，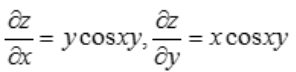

2、若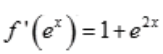，且f（0）＝1，则f(x)＝（）。

答 案：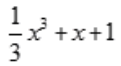

解 析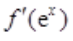：＝1＋e^2x，等式两边对e^x积分有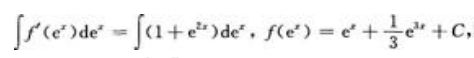所以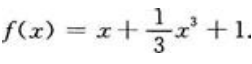

3、微分方程y'＝x＋1的通解为y＝（）。

答 案：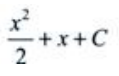

解 析：方程为可分离变量方程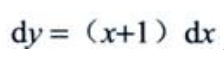，，等式两边分别积分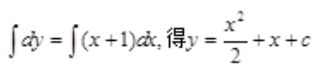

简答题

1、求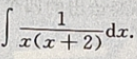  

答 案：