2025年成考专升本《高等数学一》每日一练试题05月15日
精选习题
2025-05-15
11:32:55
收藏
单选题
1、设f(x)为可导函数,则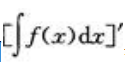 等于()。
等于()。
- A:f(x)
- B:f(x)+C
- C:
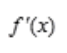
- D:
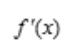 +C
+C
答 案:A
解 析:先积分后求导,积分出来的C求导后就没有了,不改变函数.若先求导后积分,这时候会产生一个常数C,这里的常数不一定是当时的那个常数。
2、若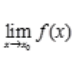 存在,
存在,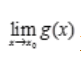 不存在,则()。
不存在,则()。
- A:
 与
与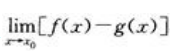 都不存在
都不存在 - B:
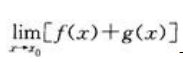 与
与 都存在
都存在 - C:
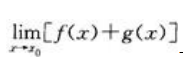 与
与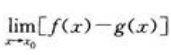 之中的一个存在
之中的一个存在 - D:
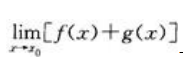 存在与否与f(x),g(x)的具体形式有关
存在与否与f(x),g(x)的具体形式有关
答 案:A
解 析:根据极限的四则运算法则可知: ,
,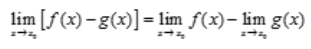 ,所以当
,所以当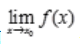 存在,
存在,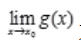 不存在时,
不存在时,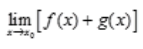 ,
,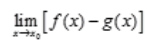 均不存在。
均不存在。
3、微分方程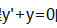 的通解为y=()。
的通解为y=()。
- A:e-x+C
- B:-e-x+C
- C:Ce-x
- D:Cex
答 案:C
解 析:所给方程为可分离变量方程。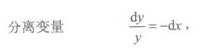
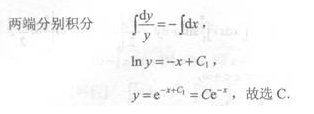
主观题
1、求微分方程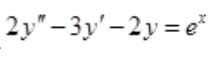 的通解。
的通解。
答 案:解: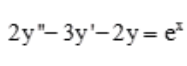 的特征值方程为
的特征值方程为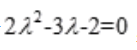 ,则
,则 ;故齐次微分方程的通解为
;故齐次微分方程的通解为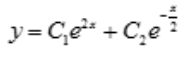 。由题意设原微分方程的特解为
。由题意设原微分方程的特解为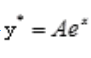 ,则有
,则有 ,得
,得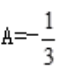 。即微分方程的通解为
。即微分方程的通解为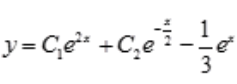 。
。
2、求函数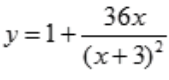 的凹凸性区间及拐点.
的凹凸性区间及拐点.
答 案:解:函数的定义域为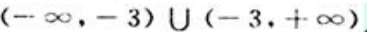 。
。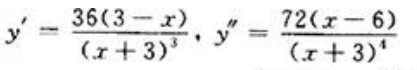 .令y″=0,得x=6;不可导点为x=-3。故拐点为(6,
.令y″=0,得x=6;不可导点为x=-3。故拐点为(6,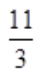 ),(-∞,-3)和(-3,6)为凸区间,(6,+∞)为凹区间。
),(-∞,-3)和(-3,6)为凸区间,(6,+∞)为凹区间。
3、设函数,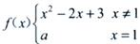 在x=1处连续,求a。
在x=1处连续,求a。
答 案:解:f(x)在x=1处连续,有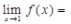
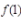 ,
,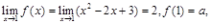
得a=2。
填空题
1、过点M0(1,-2,0)且与直线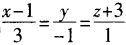 垂直的平面方程为()。
垂直的平面方程为()。
答 案:3(x-1)-(y+2)+z=0(或3x-y+z=5)。
解 析:本题考查的知识点为平面与直线的方程。由题设条件可知应该利用点法式方程来确定所求平面方程。 
2、微分方程 的通解是()。
的通解是()。
答 案: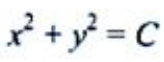
解 析:分离变量,得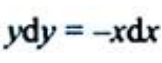 ,两边同时积分,有
,两边同时积分,有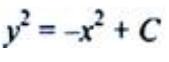 。
。
3、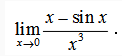
答 案: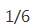
简答题
1、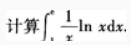
答 案: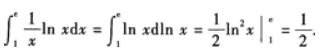
更多推荐

