2025年成考专升本《高等数学二》每日一练试题05月09日
精选习题
2025-05-09
11:26:38
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析:
单选题
1、设函数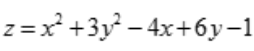 ,则驻点坐标为().
,则驻点坐标为().
- A:(2,-1)
- B:(2,1)
- C:(-2,-1)
- D:(-2,1)
答 案:A
解 析:令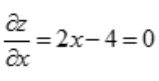 与
与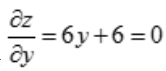 ,可得x=2,y=-1,故驻点为(2,-1).
,可得x=2,y=-1,故驻点为(2,-1).
2、已知函数f(x)在区间(-∞,+∞)上单调增加,则使f(x)>f(2)成立的x的取值范围是().
- A:(2,+∞)
- B:(-∞,0)
- C:(-∞,2)
- D:(0,2)
答 案:A
解 析:因为函数f(x)在区间(-∞,+∞)上单调增加,故当x>2时,f(x)>f(2).
主观题
1、求一个正弦曲线与x轴所围成图形的面积(只计算一个周期的面积).
答 案:解:取从0~2π的正弦曲线如图 ,设所围图形面积为S,则
,设所围图形面积为S,则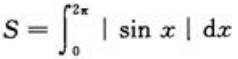
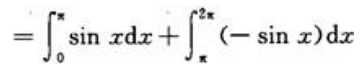
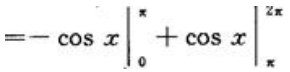
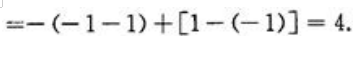 注意到图形面积是对称的,可直接得出
注意到图形面积是对称的,可直接得出 。
。
2、在半径为R的半圆内作一内接矩形,其中的一边在直径上,另外两个顶点在圆周上(如图所示).当矩形的长和宽各为多少时矩形面积最大?最大值是多少?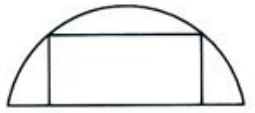
答 案:解:如图所示 ,设x轴通过半圆的直径,y轴垂直且平分直径.设OA=x,则AB=
,设x轴通过半圆的直径,y轴垂直且平分直径.设OA=x,则AB= ,矩形面积
,矩形面积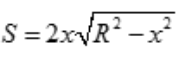 .
.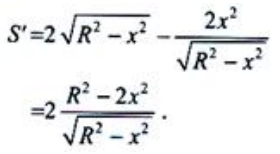 令s'=0,得
令s'=0,得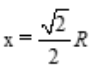 (舍去负值).
(舍去负值).
由于只有唯一驻点,根据实际问题x=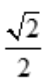 ,必为所求,则AB=
,必为所求,则AB=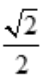 R.所以,当矩形的长为
R.所以,当矩形的长为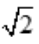 R、宽为
R、宽为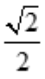 R时,矩形面积最大,且最大值S=R2.
R时,矩形面积最大,且最大值S=R2.
填空题
1、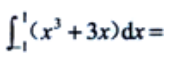 ().
().
答 案:
解 析:因为积分区间关于原点对称,被积函数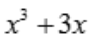 为奇函数,故
为奇函数,故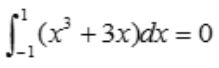 .
.
2、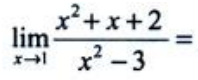 ().
().
答 案:-2
解 析: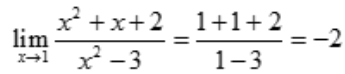 .
.
简答题
1、求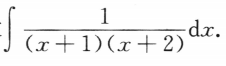
答 案: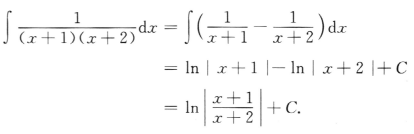
2、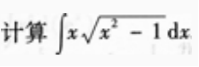
答 案: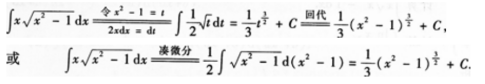
更多推荐

