2025年成考专升本《高等数学一》每日一练试题05月03日
精选习题
2025-05-03
11:40:59
收藏
单选题
1、幂级数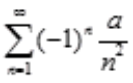 (式中a为正常数)()。
(式中a为正常数)()。
- A:绝对收敛
- B:条件收敛
- C:发散
- D:收敛性与a有关
答 案:A
解 析: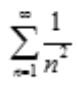 是p=2的p级数,从而知其收敛,可知
是p=2的p级数,从而知其收敛,可知 收敛,故
收敛,故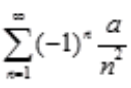 绝对收敛。
绝对收敛。
2、用待定系数法求微分方程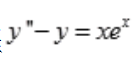 的一个特解时,特解的形式是().(式中a、b是常数)
的一个特解时,特解的形式是().(式中a、b是常数)
- A:

- B:

- C:
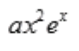
- D:
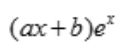
答 案:A
解 析:y″-y=0的特征方程是r2-1=0,特征根为r1=1,r2=-1.y″-y=xex中自由项f(x)=xex,a=1是特征单根,则特解为y*=x(ax+b)ex=(ax2+bx)ex。
3、下列级数中绝对收敛的是()。
- A:
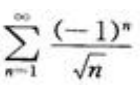
- B:
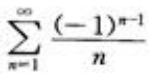
- C:
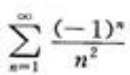
- D:

答 案:C
解 析:本题考查绝对收敛的定义.A项,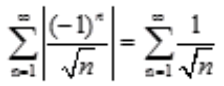 发散;B项,
发散;B项, 发散,即
发散,即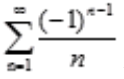 条件收敛;C项,
条件收敛;C项, 收敛;D项,
收敛;D项,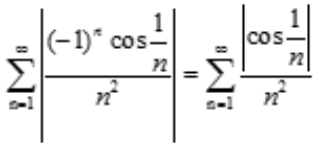 发散。
发散。
主观题
1、求微分方程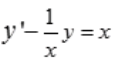 的通解。
的通解。
答 案:解: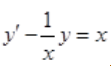 为一阶线性微分方程,则
为一阶线性微分方程,则
2、求微分方程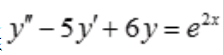 的通解.
的通解.
答 案:解:微分方程的特征方程为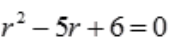 ,解得
,解得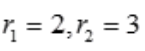 。故齐次方程的通解为
。故齐次方程的通解为 。微分方程的特解为
。微分方程的特解为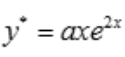 ,将其代入微分方程得
,将其代入微分方程得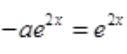 ,则a=-1。故微分方程的通解为
,则a=-1。故微分方程的通解为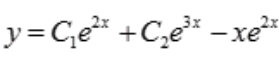 。
。
3、求函数 的极值及凹凸区间和拐点。
的极值及凹凸区间和拐点。
答 案:解: (2)令y'=0,得x1=0,x2=2。令y''=0,得
(2)令y'=0,得x1=0,x2=2。令y''=0,得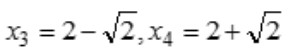 。
。
(3)列表如下:
函数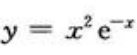 的极小值为y(0)=0,极大值为
的极小值为y(0)=0,极大值为 函数
函数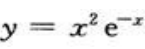 的凹区间为
的凹区间为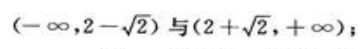 函数
函数 的凸区间为
的凸区间为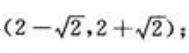 函数
函数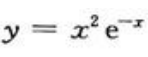 的拐点为
的拐点为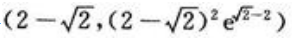 与
与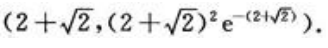
填空题
1、
答 案:2
2、设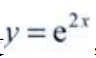 ,则
,则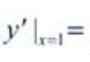 ()。
()。
答 案:2e2
解 析: ,则
,则
3、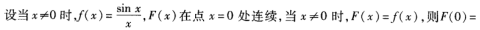 ()。
()。
答 案:1
解 析:本题考查的知识点为函数连续性的概念。 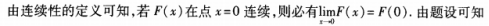
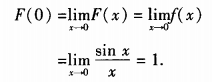
简答题
1、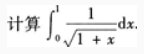
答 案: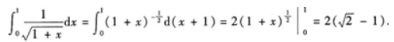
更多推荐

