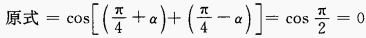单选题
1、抛物线 y=ax2的准线方程是 y=2,则a=（）。
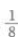
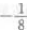
答 案：B
解 析：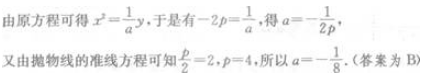
2、若a＞b＞0，则（）。
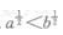
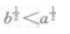
答 案：D
解 析：根据指数函数与对数函数的单调性可知,当a>b>0时,有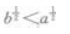
恒成立
3、下列各等式不成立的是（）。
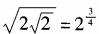
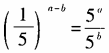
答 案：D
解 析：3x·2x=（3·2）x=6x，排除A；（3x）2=（32）x=9x，排除B；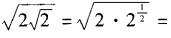
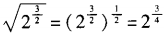，排除C。选D。
4、两个数的等差中项为20，等比中项为12，那么这两个数为（）。
答 案：C
主观题
1、已知log53=a，log54=b，求log2512关于a，b的表达式。
答 案：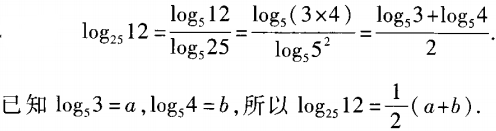
2、求下列函数的定义域： （1）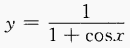
（2）
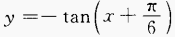
（3）
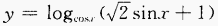
答 案：（1）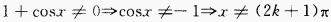 
∴函数的定义域为
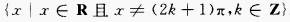（2） 
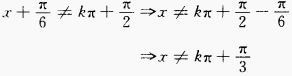∴函数的定义域为
（3）
由对数函数的性质知，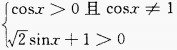
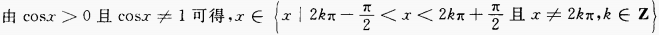
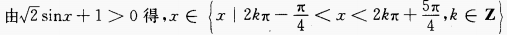故函数的定义域为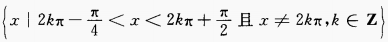
3、cos20°cos40°cos80°的值。
答 案：
4、空间有四个点，如果其中任何三点不在同一直线上，可以确定几个平面?
答 案：根据公理，在所给定的四点中任取三点，可确定一个平面，由组合公式
所以共可确定四个平面。
解 析：空间有n个点，如果其中任何三点不在同一直线上，可以确定
个平面。
填空题
1、椭圆的中心在原点，一个顶点和一个焦点分别是直线x+3y-6与两坐标轴的交点,则此椭圆的标准方程为（）
答 案：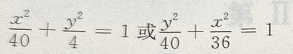
解 析：原直线方程可化为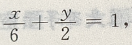
交点(6,0),(0,2). 当点(6,0)是椭圆一个焦点,点(0,2) 是椭圆一个顶点时,c=6,b=2,
当点(0,2) 是椭圆一个焦点,(6,0) 是椭圆一个顶点时,c=2,b-6,
2、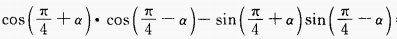
=______。
答 案：0
解 析：
