单选题
1、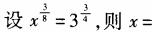
（）。
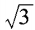
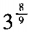
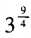
答 案：B
解 析：方法一：因为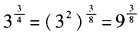
，所以
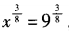，x=9，选B。 方法二：由题设，两边取以3为底的对数，得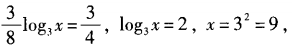 
2、从13名学生中选出2人担任正副班长，不同的选举结果共有（）。
答 案：C
3、不等式-2x2+3＜5x的解集是（）。
}
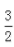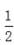或x＜-3}答 案：D
解 析：-2x2+3＜5x解：2x2-3＜-5x2x2-3+5x＞0
根据十字交叉法：
（2X-1）（X+3）＞0
解得为D
4、设甲：x＞3，乙：x＞5，则（）。
答 案：B
主观题
1、已知三角形的一个内角是
，面积是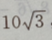
周长是20,求各边的长.
答 案：设三角形三边分别为a,b,c,∠A=60°，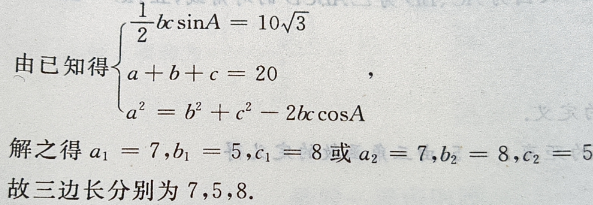 
2、已知a,b,c成等比数列，x是a，b的等差中项，y是b，c的等差中项证明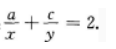
答 案：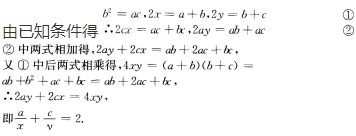
考点 本题考查考生对等差中项和等比中项公式的理解及运用．
3、每亩地种果树20棵时,每棵果树收入90元,如果每亩增种一棵,每棵果树收入就下降3元,求使总收入最大的种植棵数.
答 案：设每亩增种x棵,总收入味y元，则每亩种树(20+x)棵，由题意知增种x棵后每棵收入为（60-3x） 则有y=(90-3x)(20+x)
整理得y=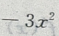
+30x+1800
配方得y=
+1875
当x=5时，y有最大值，所以每亩地最多种25棵
4、设3a=5b=15，求a-1+b-1的值。
答 案：由3a=15，得a=log315；又由5b=15，得b=log515。 因此a-1+b-1=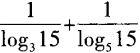
=log153+log155=1。
解 析：过程中应用了换底公式的推论，即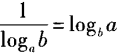
填空题
1、在等比数列中，a1=3，an=96，Sn=189，则公比q=______，项数n=_______。
答 案：q=2，n=6
解 析：解法一：An=A1×q^(n-1)=3q^(n-1)=96q^(n-1)=32S(n-1)=Sn-An=189-96=93
S(n-1)=A1×(1-q^(n-1))/(1-q)
=3(1-32)/(1-q)=93
q=2
2^(n-1)=32
n=6
解法二：
2、函数y=2cosx-cos2x（x∈R）的最大值为______。
答 案：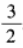
解 析：
