单选题

1、参数方程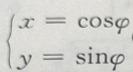（为参数）表示的图形为（）

• A：直线
• B：圆
• C：椭圆
• D：双曲线

答 案：B

解 析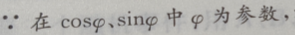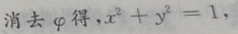：即半径为1的圆，圆心在原点

2、命题甲：实数a，b，c成等比数列；命题乙：b2＝ac，则甲是乙（）。  

• A：充分条件但不是必要条件
• B：必要条件但不是充分条件
• C：充分必要条件
• D：不是充分条件也不是必要条件

答 案：A

3、直线2x+y+m=0和直线x+2y+n=0的位置关系是（）。

• A：平行
• B：垂直
• C：相交但不垂直
• D：不确定

答 案：C

解 析：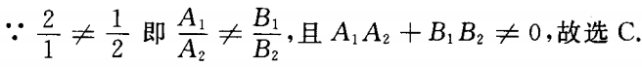

4、设函数f(x)＝e^x，则f(x－a)·f(x＋a)＝（）。

• A：f(x²－a²)
• B：2f(x)
• C：f(x²)
• D：f²(x)

答 案：D

主观题

1、某工厂每月生产x台游戏机的收入为R(x)=+130x-206(百元)，成本函数为C(x)=50x+100(百元)，当每月生产多少台时,获利润最大?最大利润为多少?  

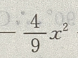答 案：利润 =收入-成本， L(x)=R(x)-C(x)=+130x-206-(50x+100)=+80x-306 法一：用二次函数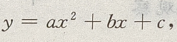当a<0时有最大值 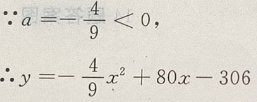是开口向下的抛物线，有最大值 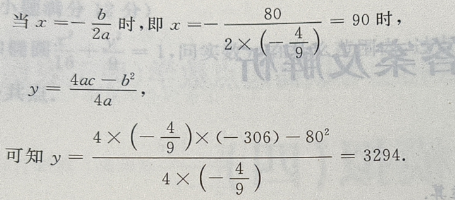法二：用导数来求解 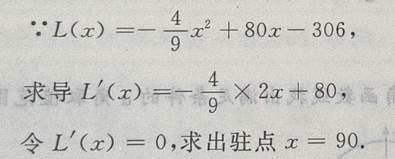因为x=90是函数在定义域内唯一驻点 所以x=90是函数的极大值点，也是函数的最大值点，其最大值为L（90）=3294  

2、已知a^m=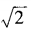，an=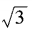，求a3^n-4m的值。  

答 案：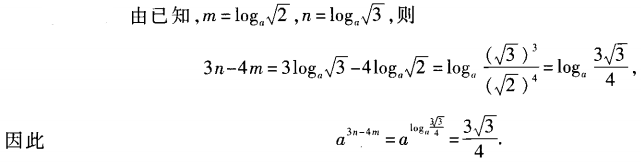

3、已知x+x^-1=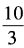，求x²+x-2的值。

答 案：由已知，得

4、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得AB=120m,求河的宽

答 案：如图， ∵∠C=180°-30°-75°=75° ∴△ABC为等腰三角形，则AC=AB=120m 过C做CD⊥AB,则由Rt△ACD可求得CD==60m， 即河宽为60m  

填空题

1、与已知直线 7x+24y-5 =0 平行，且距离等于3的直线方程是______。  

答 案：7x+24y+70=0或7z+24y-80-0

解 析：

2、y=lg（sinx）的定义域是______。  

答 案：2kπ＜x＜(2k+1)π(k∈Z)

解 析：sinx＞0∴x属于第一、二象限,所以 2kπ＜x＜(2k+1)π(k∈Z)