2025年成考高起点《数学(文史)》每日一练试题04月24日
精选习题
2025-04-24
12:00:29
收藏
单选题
1、设集合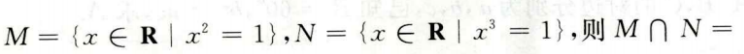 ()。
()。
- A:{1}
- B:{-1}
- C:{—1,1)
- D:
答 案:A
解 析:本题主要考查的知识点为集合的运算。 由题意M={-1,1},N={1},所以M∩N=(1}。
2、若向量a=(1,-1),b=(1,x),且|a+b|=2,则x=()。
- A:-4
- B:-1
- C:1
- D:4
答 案:C
解 析: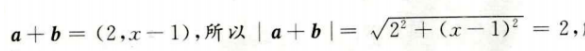 解得x=1 本题主要考查的知识点为向量的加法和模。
解得x=1 本题主要考查的知识点为向量的加法和模。
3、已知等比数列a1=1,a9=25,则a5=()。
- A:25
- B:-5
- C:±5
- D:5
答 案:C
4、在Rt△ABC中,两个锐角∠A∠B,则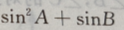
- A:有最大值
 ,无最小值
,无最小值 - B:有最大值2,最小值

- C:无最大值,有最小值

- D:既无最大值又无最小值
答 案:A
解 析:在Rt△ABC中,A、B两锐角互余,所以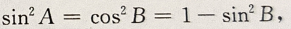
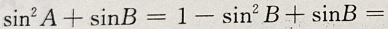
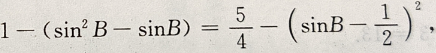
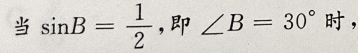

主观题
1、设椭圆的中心是坐标原点,长袖在x轴上,离心率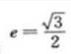 ,已知点P(0,3/2)到椭圆上的点的最远距离是
,已知点P(0,3/2)到椭圆上的点的最远距离是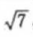 ,求椭圆的方程。
,求椭圆的方程。
答 案:
2、已知lg2=a,lg3=b,求lg0.15关于a,b的表达式。
答 案: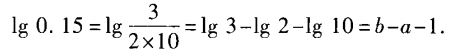
3、已知直线l的斜率为1,l过抛物线C: 的焦点,且与C交于A,B两点.
的焦点,且与C交于A,B两点.
(I)求l与C的准线的交点坐标;
(II)求|AB|.
答 案:(I)C的焦点为 ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 得
得 设A(x1,y1).B(x2,y2),则
设A(x1,y1).B(x2,y2),则 因此
因此
4、在△ABC中,已知三边 a、b、c 成等差数列,且最大角∠A是最小角的2倍, a: b :c.
答 案: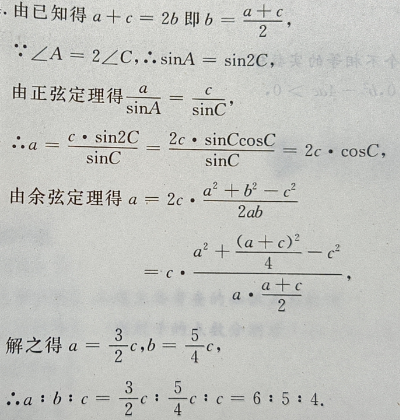
填空题
1、已知tanα=2,则 =______。
=______。
答 案:
2、设 则
则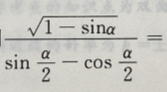
答 案:-1
解 析: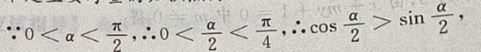
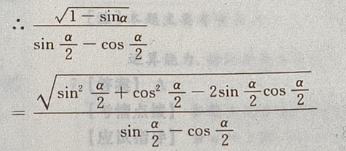
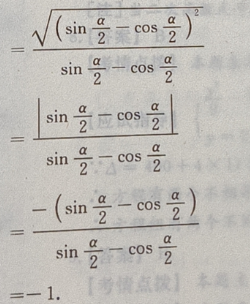
更多推荐

