2025年成考高起点《数学(理)》每日一练试题04月20日
精选习题
2025-04-20
12:23:04
收藏
单选题
1、两个数的等差中项为20,等比中项为12,那么这两个数为()。
- A:18,22
- B:9,16
- C:4,36
- D:16,24
答 案:C
2、下列各式中,不成立的是()。
- A:
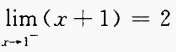
- B:
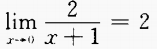
- C:
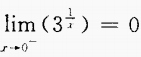
- D:
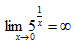
答 案:D
解 析:可用排除法,A、B、C均成立。
3、两条直线是异面直线的充分条件是这两条直线()。
- A:分别在两个平面内
- B:是分别在两个相交平面内的不相交的直线
- C:是分别在两个相交平面内的不平行的直线
- D:分别在两个相交平面内,其中一条与这两个平面的交线相交于一点,而另一条不过这个点
答 案:D
4、等差数列{an}前n项和为Sn且S10=100 ,S30=900 ,那么S50的值等于()。
- A:2400
- B:2500
- C:2700
- D:2800
答 案:B
主观题
1、已知log53=a,log54=b,求log2512关于a,b的表达式。
答 案: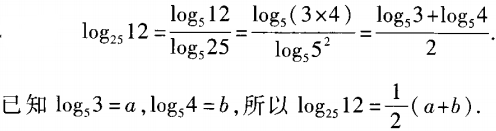
2、设 (0<α<π),求tanα的值。
(0<α<π),求tanα的值。
答 案:
3、已知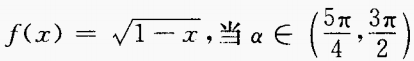 时,化简式子f(sin2α)-f(- sin2α)。
时,化简式子f(sin2α)-f(- sin2α)。
答 案:由已知得, 4、设a为实数,且tanα和tanβ是方程ax2+(2a-3)x+(a-2)=0的两个实根,求tan(α+β)的最小值。 答 案:由已知得 填空题 1、100件产品中有3件次品,每次抽取一件,有放回的抽取三次,恰有1件是次品的概率是______。
答 案:0.0847 解 析:由于三次抽取是独立的,每次抽取可看做是一次试验,每次试验只有两个可能结果:“正品”或“次品”,次品率为 2、在自然数1、2、…、100中任取一个数,该数能被3整除的概率是______。
答 案:0.33 解 析:此题随机试验包含的基本事件总数n=100,且每个数能被取到的机会均等,即属于等可能事件的概率能被3整除的自然数的个数m=33,故所求概率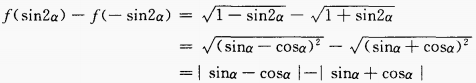
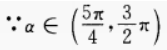 ∴sinα
∴sinα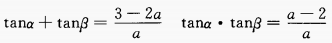

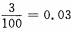 ,因此二次独立且重复试验恰有1件次品率为
,因此二次独立且重复试验恰有1件次品率为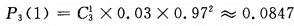
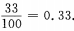
更多推荐

