单选题

1、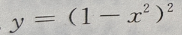的导数是  

• A：
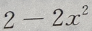
• B：
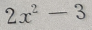
• C：
• D：

答 案：C

解 析：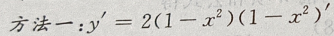

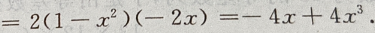
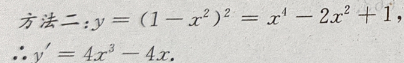
2、设集合P=（1，2，3，4，5），Q={2，4，6，8，10}，则集合P∩Q=（）。  

• A：｛2，4}
• B：｛1，2，3，4，5，6，8，10}
• C：｛2｝
• D：｛4｝

答 案：A

3、若A（-3，5），B（-5，-3），则线段AB中点的坐标为（）。  

• A：（4，-1）
• B：（-4，1）
• C：（-2，4）
• D：（-1，2）

答 案：B

4、方程x²+mx+2=0的两根为x₁和x₂，若（）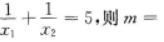

• A：-10
• B：10
• C：-5
• D：5

答 案：A

解 析：由一元二次方程根与系数的关系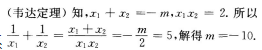

主观题

1、在△ABC中，AB=2，BC=3,B=60°，求AC及△ABC的面积

答 案：

2、已知等差数列{an}中，a1+a3+a5=6，a2+a4+a6=12，求{an}的首项与公差.  

答 案：因为{an}为等差数列，则

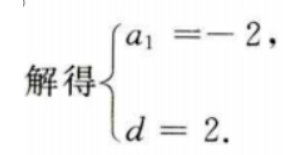
3、设函数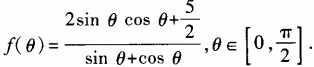 （1）求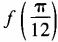；（2）求函数f（θ）最小值。

答 案：

4、弹簧的身长与下面所挂砝码的重量成正比，知弹簧挂20g重的砝码时长度是12cm,挂35g重的砝码时长度是15cm，写出弹簧长度y(cm)与砝码重x(g)的函数关系式，并求弹簧不挂砝码时的长度  

答 案：设弹簧原长为y0cm，则弹簧伸长量为（y-y0）cm。 由题意得 y-y0 =kx,即 y= kx+y0， 所求函数关系式为y=0.2x+8，弹簧的原长为8CM

填空题

1、5个同学站成一排，其中某个人恰好站在排头的概率是______。  

答 案：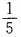

解 析：基本事件的总数n=5！，其中某人恰好站在排头的排法有m=4！种，所求概率为。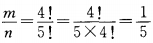  

2、在∆ABC中，已知cosA=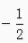，cosB=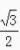，那么cosC=______。

答 案：