2025年成考专升本《高等数学一》每日一练试题03月26日
精选习题
2025-03-26
11:26:08
收藏
单选题
1、设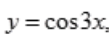 则y'=()。
则y'=()。
- A:
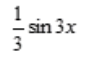
- B:
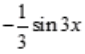
- C:
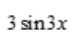
- D:
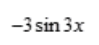
答 案:D
解 析: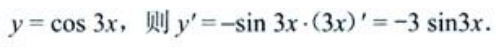
2、曲线 与其过原点的切线及y轴所围面积为()
与其过原点的切线及y轴所围面积为()
- A:
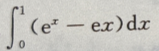
- B:

- C:
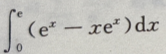
- D:

答 案:A
解 析:设(x0,y0)为切点,则切线方程为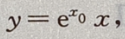 联立
联立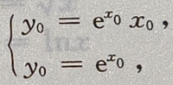 得x0=1,y0=e,所以切线方程为y=ex,故所求面积为
得x0=1,y0=e,所以切线方程为y=ex,故所求面积为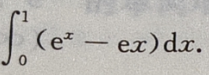
3、若f(x)为[a,b]上的连续函数,则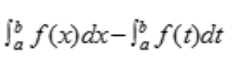 ()。
()。
- A:小于0
- B:大于0
- C:等于0
- D:不确定
答 案:C
解 析:f(x)为[a,b]上的连续函数,故 存在,它为一个确定的常数,由定积分与变量无关的性质,可知
存在,它为一个确定的常数,由定积分与变量无关的性质,可知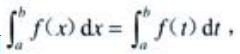 故
故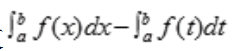 =0。
=0。
主观题
1、已知当x→0时,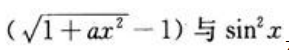 是等价无穷小量,求常数a的值。
是等价无穷小量,求常数a的值。
答 案:解:因为当x→0时,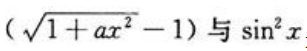 是等价无穷小量,所以有
是等价无穷小量,所以有 则
则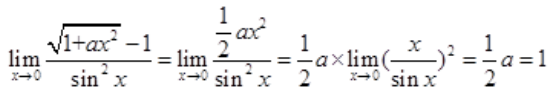 解得a=2。
解得a=2。
2、已知f(π)=1,且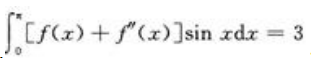 ,求f(0)。
,求f(0)。
答 案:解:
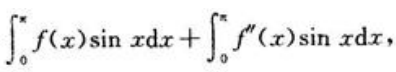 对
对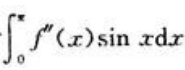 采用凑微分和分部积分后与
采用凑微分和分部积分后与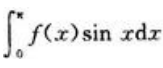 相加,代入条件即可求出f(0)。因为
相加,代入条件即可求出f(0)。因为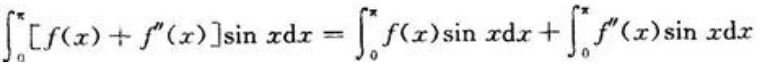
而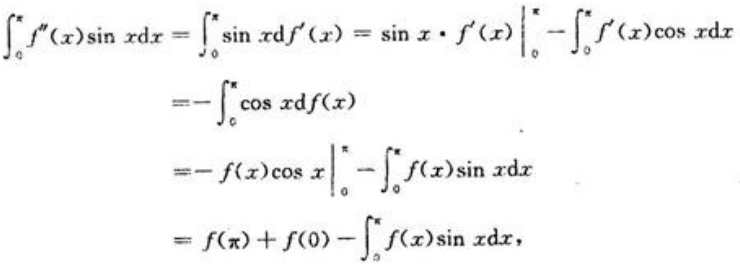
所以
又f(π)=1,所以f(0)=2。
3、设函数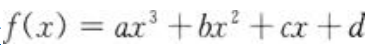 ,问常数a,b,c满足什么关系时,f(x)分别没有极值、可能有一个极值、可能有两个极值?
,问常数a,b,c满足什么关系时,f(x)分别没有极值、可能有一个极值、可能有两个极值?
答 案:解:此函数在定义域(-∞,+∞)处处可导,因此,它的极值点必是驻点即导数等于零的点,求导得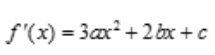 令
令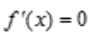 即
即 由一元二次方程根的判别式知:当
由一元二次方程根的判别式知:当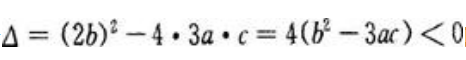 时,
时,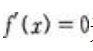 无实根。
无实根。
由此可知,当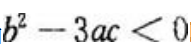 时,f(x)无极值。
时,f(x)无极值。
当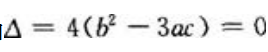 时,
时,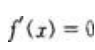 有一个实根。
有一个实根。
由此可知,当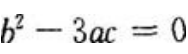 时,f(x)可能有一个极值。
时,f(x)可能有一个极值。
当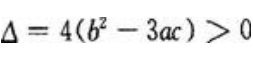 时,f(x)可能有两个极值。
时,f(x)可能有两个极值。
填空题
1、设y=(x+3)2,则y'=()。
答 案:2(x+3)
解 析: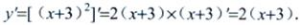
2、 ()
()
答 案: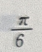
解 析: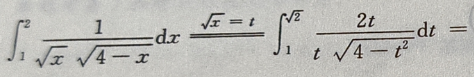
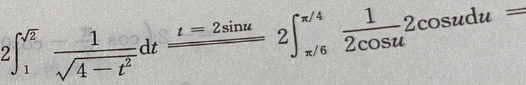
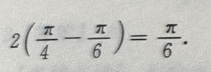
3、广义积分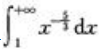 =()。
=()。
答 案: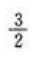
解 析: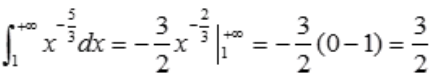 。
。
简答题
1、给定曲线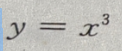 与直线y=px-q(其中p>0),求p与q为关系时,直线y=px-q
与直线y=px-q(其中p>0),求p与q为关系时,直线y=px-q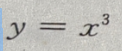 的切线。
的切线。
答 案:由题意知,再切点处有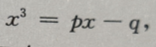 两边对x求导得
两边对x求导得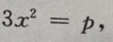

更多推荐

