单选题
1、下列函数中为奇函数的是（）。
答 案：D
解 析：对于D，f(-x)＝(-x)3＋tan(-x)＝-(x3＋tanx)＝－f(x)。答案为D。
2、抛物线 y=ax2的准线方程是 y=2,则a=（）。
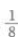
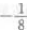
答 案：B
解 析：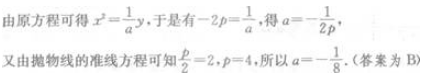
3、下列函数中，为偶函数的是（）。
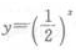
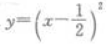
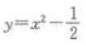
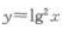
答 案：C
解 析：根据函数的奇偶性的定义可知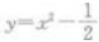
为偶函数
4、二次函数y＝2x2＋mx－5在区间(－∞，－1)内是减函数，在区间(－1，＋∞)内是增函数，则m的值是（）。
答 案：A
解 析：由题意可知二次函数y=2x2+mx-5的对称轴方程为x=-1,又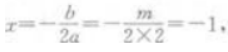
解得m=4
主观题
1、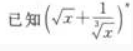
展开式的二项式系数之和比
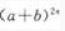展开式的二项式系数之和小240。 求：（1）
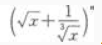展开式的第3项；
（2）
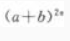展开式的中间项。
答 案：
2、cos20°cos40°cos80°的值。
答 案：
3、设
（0＜α＜π），求tanα的值。
答 案：
4、在△ABC中如果sinA=2sinBcosC，求证：△ABC是等腰三角形。
答 案：
∴△ABC为等腰三角形。
填空题
1、已知sin2θ+1=cos2θ，则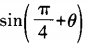
的值等于______。
答 案：
解 析：由已知，cos2θ-sin2θ=1，即cos2θ-（1-cos2θ）=1，cos2θ=1，所以cosθ=±1。 而当cosθ=±1时，sinθ=0。 
2、100件产品中有3件次品，每次抽取一件，有放回的抽取三次，恰有1件是次品的概率是______。
答 案：0.0847
解 析：由于三次抽取是独立的，每次抽取可看做是一次试验，每次试验只有两个可能结果：“正品”或“次品”，次品率为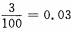
，因此二次独立且重复试验恰有1件次品率为
