单选题

1、矩阵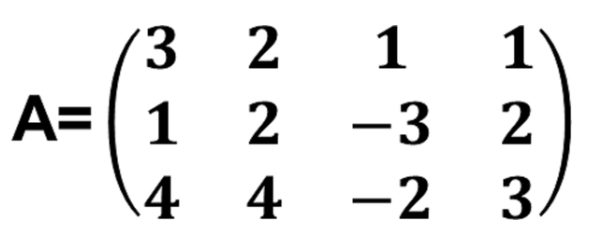的秩是（）

• A：0
• B：1
• C：2
• D：3

答 案：C

解 析：

2、设f（x）在点x₀处取得极值，则（）。

• A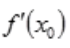：不存在或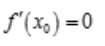
• B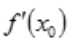：必定不存在
• C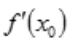：必定存在且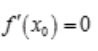
• D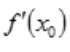：必定存在，不一定为零

答 案：A

解 析：若点x₀为f（x）的极值点，可能为两种情形之一：（1）若f（x）在点x₀处可导，由极值的必要条件可知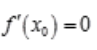；（2）如f（x）＝|x|在点x＝0处取得极小值，但f（x）＝|x|在点x＝0处不可导，这表明在极值点处，函数可能不可导。

3、（）。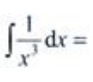

• A：
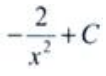
• B：
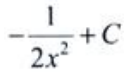
• C：
• D：

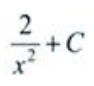
答 案：B

解 析：。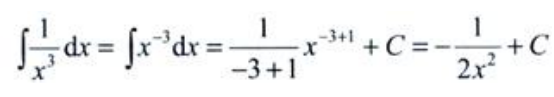

主观题

1、设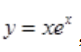，求y'．

答 案：解：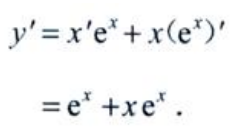

2、求。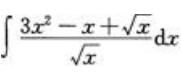

答 案：解：

3、求．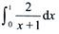

答 案：解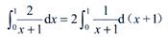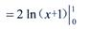：＝2ln2

填空题

1、幂级数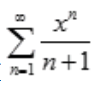的收敛半径是（）。

答 案：1

解 析：，。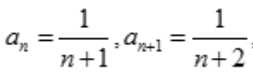

2、设y＝sin（x＋2），则y'＝（）。

答 案：cos（x＋2）

解 析：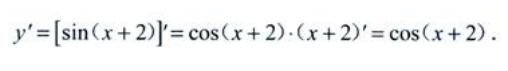

3、过点(1,0,-1)与平面3x-y-z-2=0平行的平面的方程为（）

答 案：3x-y-z-4=0

解 析：平面3x-y-z-2=0的法向量为(3，-1，-1)，所求平面与其平行，故所求的平面的法向量为(3，-1，-1)，由平面的点法式方程得所求平面方程为3(x-1)-(y-0)-(z+1)=0，及3x-y-z-4=0。

简答题

1、  

答 案：积分区域D如图2-1所示。 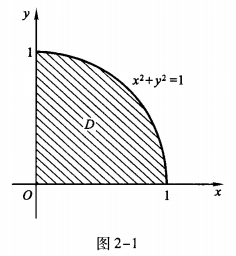解法1利用极坐标系。

解 析：本题考查的知识点为计算二重积分；选择积分次序或利用极坐标计算。