2025年成考专升本《高等数学一》每日一练试题03月14日
精选习题
2025-03-14
11:32:08
收藏
单选题
1、下列四项中,正确的是()。
- A:
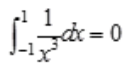
- B:
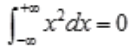
- C:
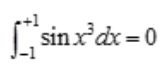
- D:
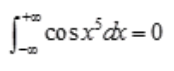
答 案:C
解 析:A项,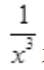 在(-1,1)不连续;B项,
在(-1,1)不连续;B项, 不存在;C项,
不存在;C项, 在(-1,1)为奇函数,所以
在(-1,1)为奇函数,所以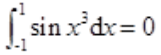 ;D项,
;D项, 也不存在。
也不存在。
2、 ()。
()。
- A:0
- B:cos2-cos1
- C:sin1-sin2
- D:sin2-sin1
答 案:A
解 析:
3、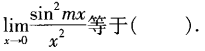
- A:1
- B:
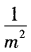
- C:m
- D:m2
答 案:D
解 析:本题考查的知识点为重要极限公式或等价无穷小量代换。 
主观题
1、设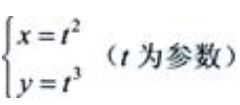 ,求
,求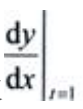
答 案:解:由题意得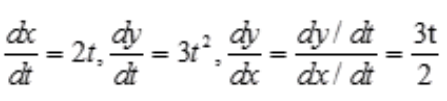 故
故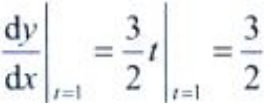 。
。
2、求微分方程y'-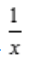 =lnx满足初始条件
=lnx满足初始条件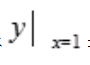 =1的特解。
=1的特解。
答 案:解:P(x)= ,Q(x)=lnx,则
,Q(x)=lnx,则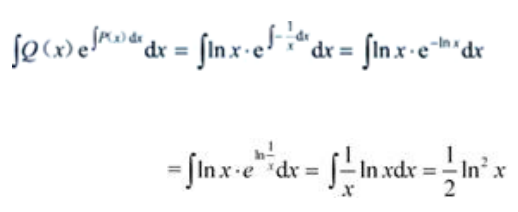 所以
所以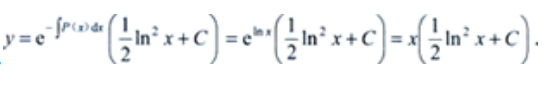 将
将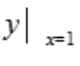 =1代入y式,得C=1.故所求特解为
=1代入y式,得C=1.故所求特解为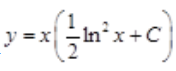 。
。
3、将函数f(x)=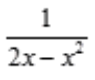 展开为x-1的幂级数,并指出收敛区间(不讨论端点)。
展开为x-1的幂级数,并指出收敛区间(不讨论端点)。
答 案:解: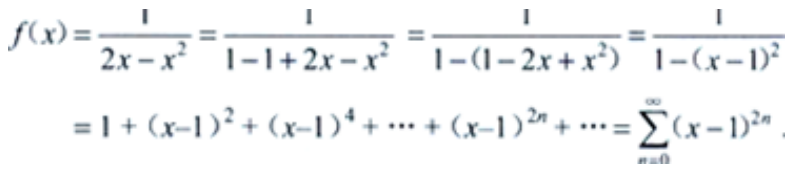 由
由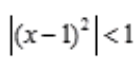 ,知-1<x-1<1,0<x<2,即收敛区间是(0,2)。
,知-1<x-1<1,0<x<2,即收敛区间是(0,2)。
填空题
1、
答 案:2
2、函数 的驻点x=()。
的驻点x=()。
答 案:e
解 析: ,令y'=0,得驻点x=e。
,令y'=0,得驻点x=e。
3、函数y=x3-2x+1在区间[1,2]上的最小值为()。
答 案:0
解 析:本题考查的知识点为连续函数在闭区间上的最小值问题。通常求解的思路为:先求出连续函数f(x)在(a,b)内的所有驻点x1,…,xk。 
简答题
1、求微分方程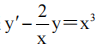 的通解.
的通解.
答 案:由题可知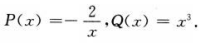 通解为
通解为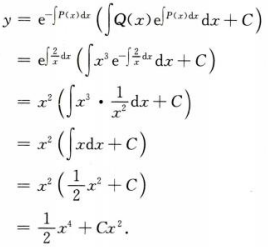
更多推荐

