2025年高职单招《数学(中职)》每日一练试题02月22日
精选习题
2025-02-22
16:04:14
收藏
单选题
1、设首项为2,公比为2的等比数列{an}的前n项和为Sn,则()
- A:

- B:

- C:

- D:

答 案:D
解 析: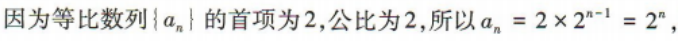
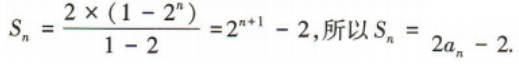
2、在等比数列{an}中,a2=9,a5=243,则{an}的前4项和为()
- A:81
- B:120
- C:168
- D:192
答 案:B
解 析:设等比数列{a}的公比为q.由题意得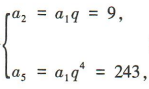 解得a1=3,q=3,故a3=a2q=27,a4=a3q=81,所以{a,}的前4项和S4=a1+a2+a3+a4=3+9+27+81=120.
解得a1=3,q=3,故a3=a2q=27,a4=a3q=81,所以{a,}的前4项和S4=a1+a2+a3+a4=3+9+27+81=120.
3、样本5,4,6,7,3的平均数和标准差分别为()
- A:5,2
- B:
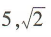
- C:6.3
- D:
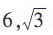
答 案:B
解 析:易得样本的平均数为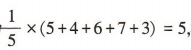 标准差为
标准差为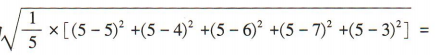
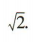
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、设集合
答 案:{x|x≤1或x≥2}
解 析:
2、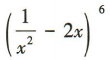 的展开式中各项系数之和为()
的展开式中各项系数之和为()
答 案:1
解 析:令x=1,得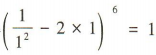 ,即
,即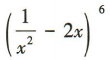 的展开式中各项系数之和为1.
的展开式中各项系数之和为1.
3、已知f(x)是一次函数,且其图像过点A(-2,0),B(1,5),则f(x)=()
答 案:
解 析: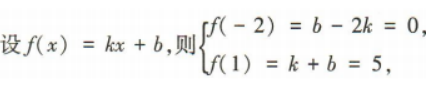

简答题
1、甲、乙两人进行投篮训练,己知甲投球命中的概率是1/2,乙投球命中的概率是3/5,且两人投球命中与否相互之间没有影响. (1) 若两人各投球1次,求恰有1人命中的概率; (2) 若两人各投球2次,求这4次投球中至少有1次命中的概率
答 案:解:记甲投球命中为事件A,甲投球未命中为事件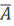 :乙投球命中为事件B,乙投球未命中为事件
:乙投球命中为事件B,乙投球未命中为事件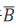 则
则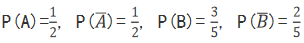 (1)记两人各投球1次,恰有1人命中为事件C,则P(C)= P(A)·P(
(1)记两人各投球1次,恰有1人命中为事件C,则P(C)= P(A)·P(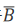 )+ P(
)+ P(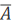 )·P(B)
=
)·P(B)
=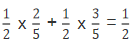 (2)记两人各投球2次,4次投球中至少有1次命中为事件D,则.两人各投球2次,4次投球中全未命中为事件
(2)记两人各投球2次,4次投球中至少有1次命中为事件D,则.两人各投球2次,4次投球中全未命中为事件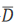
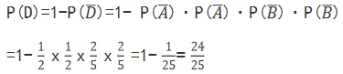
更多推荐

