单选题
1、设α=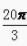
，则（）。
答 案：A
2、下列函数中，既是偶函数，又在区间（0，3）为减函数的是（）。
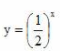
答 案：A
3、已知△ABC中，A：B：C=1：2：3，那么a：b：c为（ ）
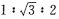
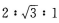
答 案：B
解 析：因为A：B：C=1：2：3，所以A=30°，B=60°，C=90°，由此可得a：b：c=
4、已知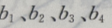
成等差数列，且
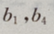为方程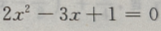
的两个根，则
的值为（）
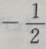
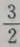
答 案：D
解 析：由根与系数的关系得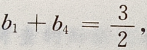
由等差数列的性质得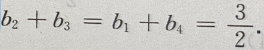
主观题
1、已知等差数列
前n项和
（Ⅰ）求通项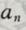
的表达式
（Ⅱ）求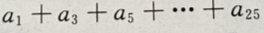
的值
答 案：（Ⅰ）当n=1时，由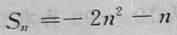
得
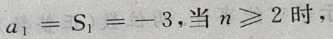
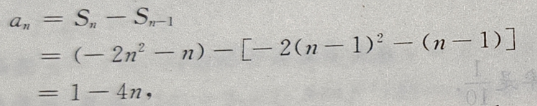
也满足上式，故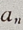
=1-4n（n≥1）
（Ⅱ）由于数列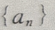
是首项为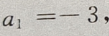
公差为d=-4的等差数列，所以
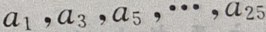是首项为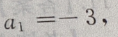
公差为d=-8，项数为13的等差数列，于是由等差数列前n项和公式得：
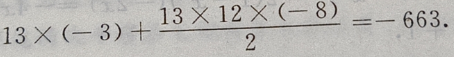
2、（1）已知tanα=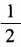
求cot2α的值； （2）已知tan2α=1，求tanα的值。
答 案：（1）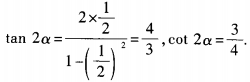
（2）由已知，得
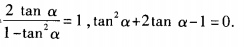解关于tanα的一元二次方程，得tanα=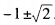
3、已知抛物线C：y2=2px（p>0）的焦点到准线的距离为1。（I）求C的方程；
（Ⅱ）若A（1，m）（m>0）为C上一点，O为坐标原点，求C上另一点B的坐标，使得OA⊥OB。
答 案：(I)由题意,该抛物线的焦点到准线的距离为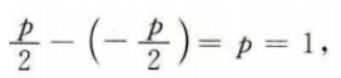
所以抛物线C的方程为y2=2x.
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得 m=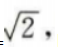
因此A点坐标为
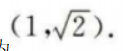设B点坐标为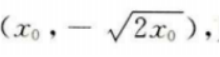
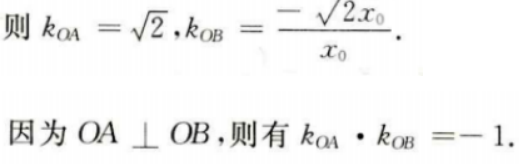
4、如图9-4，已知测速站P到公路L的距离为40米，一辆汽车在公路L上行驶，测得此车从A点行驶到8点所用的时间为2秒，并测得∠APO=60°，∠BPO=30°，计算此车从A到B的平均速度为多少km/h（结果保留到个位），并判断此车是否超过了80km/h的限制速度。
答 案：此车从A到B的平均速度为83（km/h），已经超过80km/h的限制速度。
填空题
1、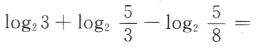
（）
答 案：3
解 析：
2、函数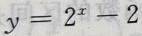
的图像与坐轴的交点共有（）个
答 案：2
解 析：当x=0，
故函数与y轴交于(0,-1)点;令y=0,则有
故函数与工轴交于(1,0)点,因此函数
与坐标轴的交点共有2个
