单选题
1、函数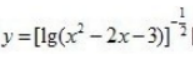
定义域为（）。
答 案：D
2、设函数f(x)＝ex，则f(x－a)·f(x＋a)＝（）。
答 案：D
3、二次函数y＝2x2＋mx－5在区间(－∞，－1)内是减函数，在区间(－1，＋∞)内是增函数，则m的值是（）。
答 案：A
解 析：由题意可知二次函数y=2x2+mx-5的对称轴方程为x=-1,又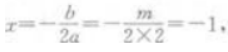
解得m=4
4、已知圆的方程为x2＋y2－2x＋4y＋1＝0，则圆上一点到直线3x＋4y－10＝0的最大距离为（）。
答 案：B
解 析：圆x2+y2-2x+4y+1=0,即(x-1)2+(y+2)2=22的圆心为(1,-2)半径r=2，
圆心(1.-2)到直线3x＋4y－10＝0的距离是
圆上一点到直线3x+4y-10=0的距离的最大值是3+2=5.(答案为B)
主观题
1、求函数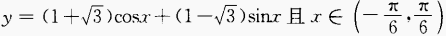
上的最大值以及取得这个最大值的x。
答 案：.1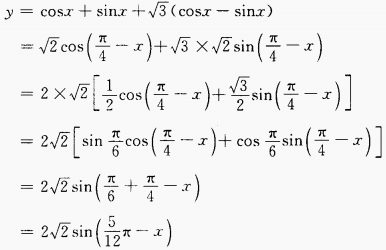 
函数取最大值，即y最大值=。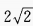
2、在正四棱柱ABCD-A'B'C'D'中，
（Ⅰ）写出向量
关于基底{a,b,c}的分解式
（Ⅱ）求证：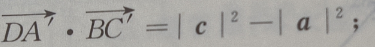
（Ⅲ）求证：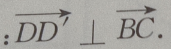
答 案：(Ⅰ)由题意知(如图所示)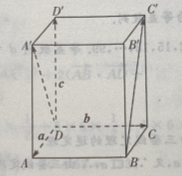 
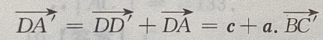
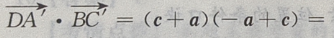
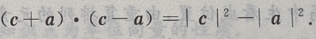(Ⅱ)
(Ⅲ)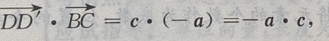
由已知，a,c是正四棱柱的棱，a,b,c两两垂直
3、求将抛物线y=x2-2x-3平移到顶点与坐标原点重合时的函数解析式。
答 案：
4、设函数f(x)=
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
答 案：(Ⅰ)函数的定义域为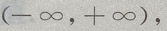
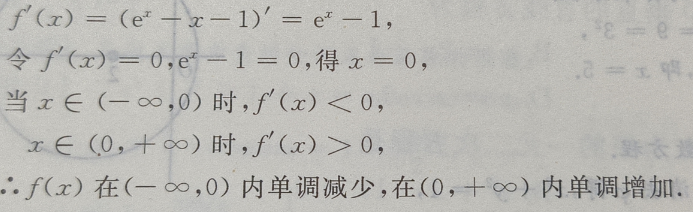(Ⅱ)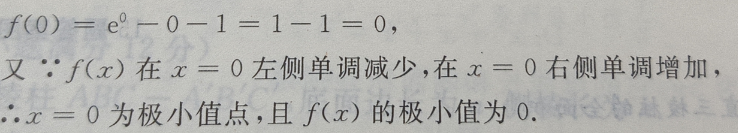
填空题
1、若平面向量a=(x,1),b=(1,-2),且a//b,则x=（）
答 案：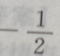
解 析：由于a//b，故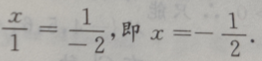
2、一个问题在1小时内，甲能独立解决的概率是0.5，乙能独立解决的概率是0.4，两人在1小时内解决问题的概率是______。
答 案：0.7
解 析：设事件A为两人在1小时内解决问题，即1小时内至少有一人能解决问题，事件B为甲在1小时内解决问题，事件C为乙在1小时内解决问题，事件B、C是相互独立事件，事件A的对立事件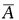
互为在1小时内两个人都没有解决问题，所以 P（A）=1-P（
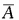）=1-P（
·
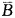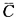）=1-P（
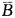）·P（
）
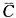=1-（1-0.5）×（1-0.4）=1-（0.5×0.6）=1-0.3=0.7
