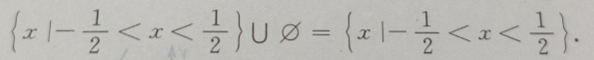单选题
1、曲线y=x+2在点（1，2）处的切线斜率为（）。
答 案：A
解 析：方法一：∵y=x+2，k=y’＝1 方法二：也可用直线方程y=kx+b直接得出k=1。
2、抛物线y2＝4x上一点P到焦点F的距离是10，则点P坐标是（）。
答 案：B
解 析：抛物线y2=4x的焦点为F(1,0),设点P坐标是(z,y),则有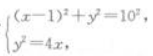
解方程组,得x=9,y=±6,即点P坐标是(9,±6).(答案为B)
3、在△ABC中,已知2B= A+C,
= ac,则B-A=（）
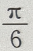
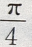
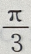
答 案：A
解 析：在△ABC中,A+B+C=π，A+C=π-B，① 因为2B=A+C，②
由①②得2B=π-B，
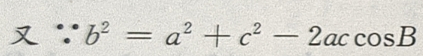
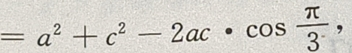
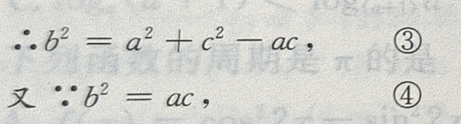由③④得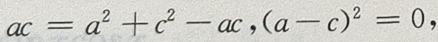
a=c。所以A=C，又
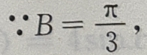所以△ABC为等边三角形，则B-A=0
4、设函数f(x)＝ex，则f(x－a)·f(x＋a)＝（）。
答 案：D
主观题
1、记△ABC的内角A，B，C的对边分别为a，b，c，已知B=60°，b2=ac，求A。
答 案：由余弦定理b2=a2+c2-2accosB，可得ac=a2+c2-ac，即a2+c2-2ac=(a-c)2=0，解得a=c。 又因为B=60°，故△ABC为等边三角形，所以A=60°
2、在正四棱柱ABCD-A'B'C'D'中，
（Ⅰ）写出向量
和
关于基底{a,b,c}的分解式;
（Ⅱ）求证：
（Ⅲ）求证：
答 案：（Ⅰ）由题意知(如图所示)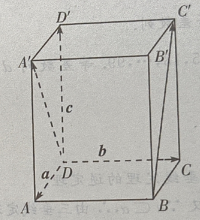 
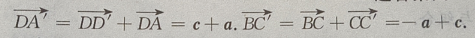
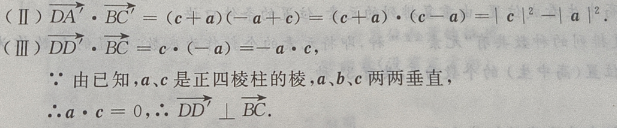
3、（1）已知tanα=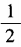
，求cot2α的值； （2）已知tan2α=1，求tanα的值。
答 案：（1）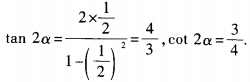
（2）由已知，得
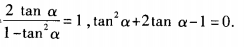解关于tanα的一元二次方程，得tanα=
4、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得
AB=120m,求河的宽
答 案：如图， 
∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形，则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD=
=60m，
即河宽为60m
填空题
1、已知函数y=a2+bx+c的图像是以(6,-12)为顶点的抛物线，并且与x轴的一个交点坐标是(8,0)，则a=()，b=()，c=()
答 案： 3；-36；96
解 析：根据顶点坐标是（6，-12），设y=a(x-6)2-12(8,0)代入得：0=a*(8-6)2-12得到a=3
即y=3(x-6)2-12=3x2-36x+96
故a=3,b=-36,c=96
2、不等式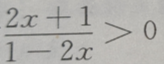
的解集为（）
答 案：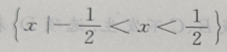
解 析：
