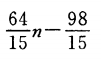判断题

1、一个游戏的中奖概率是0.1，则做10次这样的游戏一定会中奖。()  

答 案：错

解 析：一个游戏的中奖概率是0.1，则做10次这样的游戏一定会中奖，此题是随机事件，不一定就中奖，此说法错误。

2、双曲线的焦点一定在实轴上。（）  

答 案：对

解 析：双曲线与坐标轴两交点的连线段AB叫做实轴。实轴的长度为2a

单选题

1、已知点P是圆（x-3）²+y²=1上的动点，则P到直线y=x+1的距离最小是多少？（）  

• A：3
• B：
• C：
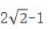
• D：

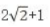
答 案：C

2、 函数f（x）=e^x-2-2的零点所在的区间是（）  

• A：(0,1)
• B：(1,2)
• C：(2,3)
• D：(3,4)

答 案：C

解 析：计算得到f（2）f(3)＜0即得解由题得f（2）f(3)＜0即得解。由题得f（2）=e^2-2-2=-1＜0，f(3)=e^3-2-2＞0，所以f(2)f(3)＜0所以f(2)f（3）＜0，所以函数f(x)=e^x-2-2的零点所在的区间是（2，3）。故选：C

多选题

1、设等差数列{a_n}的公差为d，其前n项和为S_n，且a₁=-5，S₃=-9，则（）  

• A：d=2
• B：S₂，S₄，S₆为等差数列
• C：数列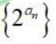是等比数列
• D：S₃是S_n的最小值

答 案：ACD

2、已知函数y=1/2sin2x则（）  

• A：函数最大值为2
• B：函数最大值为1/2
• C：周期
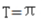
• D：周期

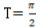
答 案：BC

解 析：A：sin2x最大值为1，则y=1/2sin2x的最大值为1/2，故A错B对。C：T=2π/W=2π/2=π，故C对D错

主观题

1、已知等差数列{an}的前n项和S_n且S₅=35,S₈=104.
(1)求数列{an}的通项公式；
(2)若{b_n}为等比数列，b₁=a₂,b₂=a₃+2,求数列{b,}的公比q及前n项和T_n.

答 案：(1)所以a₆=19.则数列{an}的公差，通项公式为an=a₆+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以则

2、已知两直线,当m为何值时，l₁与l₂: (1)相交；(2)平行；(3)重合.  

答 案：(1)当1×3m-(m-2)m²=-m²(m-2)+3m=-m(m-3)(m+1)≠0时，l₁与l₂相交，即m≠0,m≠3且m≠-1. (2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时，l₁与l₂平行，即m=0或m=-1. (3)当-m(m-3)(m+1)=0且12-4m=0时，l₁与l₂重合，即m=3.

填空题

1、  

答 案：5

解 析：

2、在数列{a_n}中， a₂=2,a₁₇=66,通项公式是项数n的一次式，则 a_n=______ .

答 案：