单选题
1、已知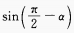
=
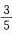，则
=（）。
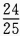
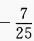
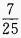
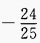
答 案：C
解 析：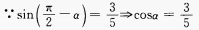
2、中心在坐标原点，对称轴为坐标轴，且一个顶点（3，0），虚轴长为8的双曲线方程是（）
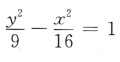
答 案：B
解 析：双曲线有一个顶点为(3,0)，因此所求双曲线的实轴在x轴上，可排除A、C选项，又由于虚轴长为8，故b=4，即b2=16，故双曲线方程为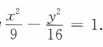
3、曲线y=x+2在点（1，2）处的切线斜率为（）。
答 案：A
解 析：方法一：∵y=x+2，k=y’＝1 方法二：也可用直线方程y=kx+b直接得出k=1。
4、下列函数中为奇函数的是（）。
答 案：D
解 析：对于D，f(-x)＝(-x)3＋tan(-x)＝-(x3＋tanx)＝－f(x)。答案为D。
主观题
1、已知a,b,c成等差数列，a,b,c+1成等比数列．若b=6，求a和c．
答 案：由已知得
解得
2、设函数f(x)=
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
答 案：(Ⅰ)函数的定义域为
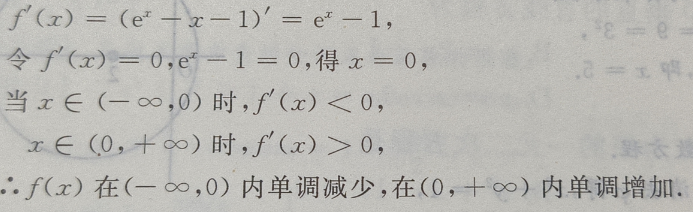(Ⅱ)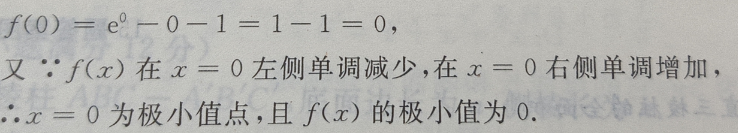
3、试证明下列各题
（1）
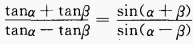
（2）
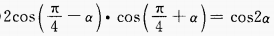
答 案：（1）化正切为正、余弦，通分即可得证。 （2）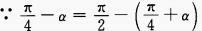
4、已知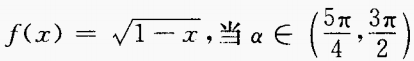
时，化简式子f(sin2α)-f(- sin2α)。
答 案：由已知得， 填空题 1、若P（3，2）是连接P1（2，y）和P2（x，6）线段的中点，则x=______，y=______。
答 案：x=4，y=-2
解 析： 2、椭圆的中心在原点，一个顶点和一个焦点分别是直线x+3y-6与两坐标轴的交点,则此椭圆的标准方程为（）
答 案： 解 析：原直线方程可化为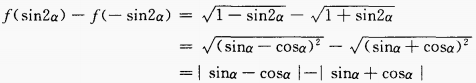
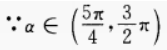∴sinα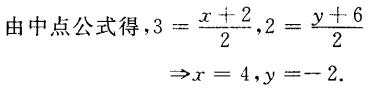
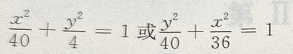
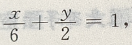交点(6,0),(0,2). 当点(6,0)是椭圆一个焦点,点(0,2) 是椭圆一个顶点时,c=6,b=2,
当点(0,2) 是椭圆一个焦点,(6,0) 是椭圆一个顶点时,c=2,b-6,
