单选题
1、在等比数列{an}中，a2=1，公比q=2，则a5=（）。
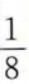
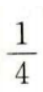
答 案：D
解 析：本题主要考查的知识点为等比数列。
2、若集合M={（x，y）｜3x-2y=-1}，N={（x，y）｜2x+3y=8}，则M∩N=（）。
答 案：C
解 析：M，N都是点集，所以只能选C。
3、已知一个等差数列的第五项等于10，前三项的和等于3，那么这个等差数列的公差为（）。
答 案：A
4、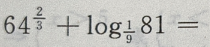
（）
答 案：B
解 析：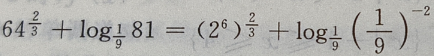
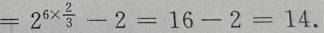
主观题
1、弹簧的身长与下面所挂砝码的重量成正比，知弹簧挂20g重的砝码时长度是12cm,挂35g重的砝码时长度是15cm，写出弹簧长度y(cm)与砝码重x(g)的函数关系式，并求弹簧不挂砝码时的长度
答 案：设弹簧原长为y0cm，则弹簧伸长量为（y-y0）cm，
由题意得y-y0=kx,即y=kx+y0,
由已知条件得
解得k=0.2，y0=8.
所求函数关系式为y=0.2x+8，弹的原长为8CM
2、设全集U=R，集合A={x｜-5＜x＜5}，B={x｜0≤x≤7}，求CUA∩B．
答 案：解：全集U=R，A={x｜-5＜x＜5}，B=｛X｜0≤x≤7}，因为CuA={x｜x≤-5或x≥5}，所以CuA∩B={x｜x≤-5或x≥5}N{x｜0≤x≤7}={x｜5≤x≤7}，如图1—10所示。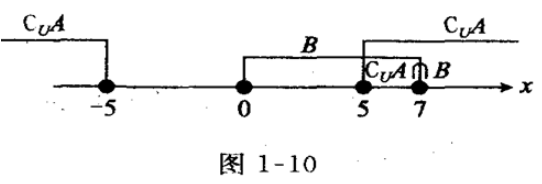
3、在△ABC中，B=120°,C=30°,BC=4，求△ABC的面积．
答 案：因为A= 180°-B-C=30°，所以AB = BC=4.因此△ABC的面积
4、已知x+x-1=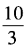
，求x2+x-2的值。
答 案：由已知，得
填空题
1、设
则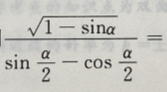
答 案：-1
解 析：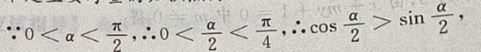
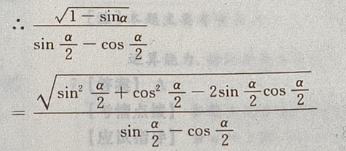
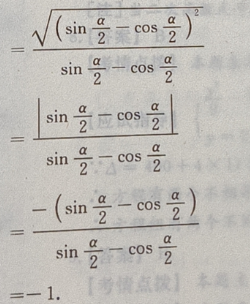
2、5个同学站成一排，其中某个人恰好站在排头的概率是______。
答 案：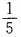
解 析：基本事件的总数n=5！，其中某人恰好站在排头的排法有m=4！种，所求概率为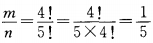
。
