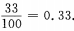单选题
1、如果点A(1，1)和B(2，4)关于直线y=kx+b对称，则k=（）。
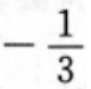
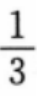
答 案：B
解 析：本题主要考查的知识点为两垂直直线斜率的关系。直线AB的斜率为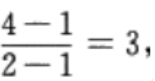
点A、B关于直线y=kx+b对称，因此直线AB与其垂直，故3k=-1，得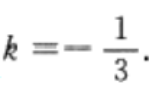
2、若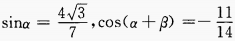
，且α、β均为锐角，则β的值为（）。
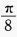
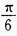
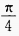
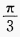
答 案：D
解 析：
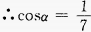
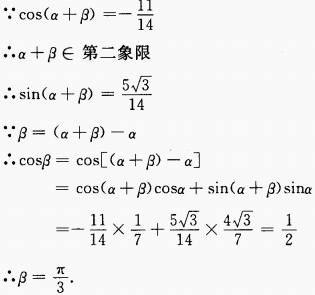
3、设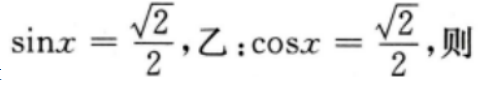
（）
答 案：D
解 析：本题主要考查的知识点为简易逻辑 由于
故甲既不是乙的充分条件，也不是乙的必要条件
4、如果球的大圆面积增为原来的4倍，则该球的体积就增为原来的（）。
答 案：B
解 析：
主观题
1、求下列函数的最大值、最小值和最小正周期： （1）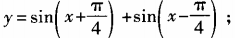
（2）y=6cosx+8sinx
答 案：
2、已知函数f(x)=(x-4)(x2-a) （I）求f"(x)； (Ⅱ)若f"(-1)=8，求f(x)在区间[0，4]的最大值与最小值
答 案：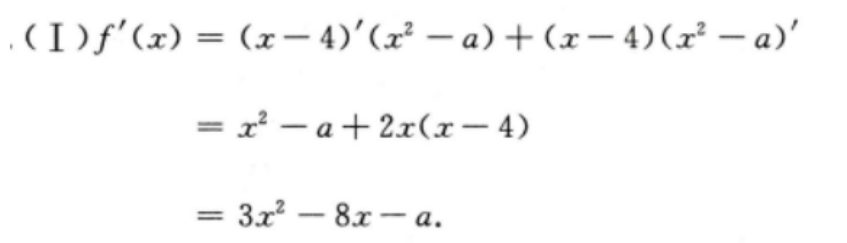
3、已知直线l的斜率为1，l过抛物线C：
的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
(II）求|AB|.
答 案：(I）C的焦点为
，准线为
由题意得l的方程为
因此l与C的准线的交点坐标为
(II）由
，得
设A（x1,y1），B（x2,y2），则
因此
4、试证明下列各题
（1）
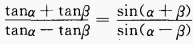
（2）
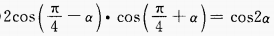
答 案：（1）化正切为正、余弦，通分即可得证。 （2）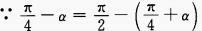
填空题
1、若平面向量a=(x,1),b=(1,-2),且a//b,则x=（）
答 案：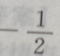
解 析：由于a//b，故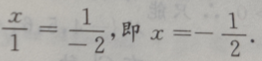
2、在自然数1、2、…、100中任取一个数，该数能被3整除的概率是______。
答 案：0.33
解 析：此题随机试验包含的基本事件总数n=100，且每个数能被取到的机会均等，即属于等可能事件的概率能被3整除的自然数的个数m=33，故所求概率
