单选题

1、曲线y＝x²＋5x＋4在点（－1，0）处切线的斜率为（）。

• A：2
• B：－2
• C：3
• D：－3

答 案：C

解 析：点（－1，0）在曲线y＝x²＋5x＋4上，y'＝2x＋5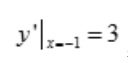，，由导数的几何意义可知，曲线y＝x²＋5x＋4在点（－1，0）处切线的斜率为3。

2、若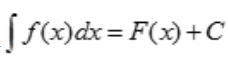，则＝（）。

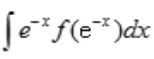• A：F（e^-x）＋C
• B：F（e^x）＋C
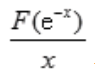• C：＋C
• D：-F（e^-x）＋C

答 案：D

解 析：由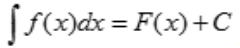，可得。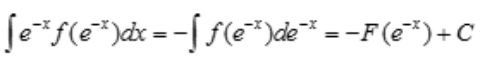

3、微分方程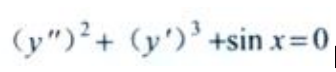的阶数为（）。

• A：1
• B：2
• C：3
• D：4

答 案：B

解 析：所给方程含有未知函数y的最高阶导数是2阶，因此方程的阶数为2。

主观题

1、求微分方程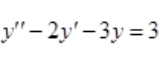的通解．

答 案：解：原方程对应的齐次微分方程为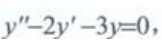特征方程为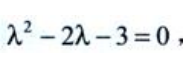特征根为x₁＝-1，x₂＝3，
齐次方程的通解为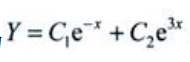
设原方程的特解为＝A，代入原方程可得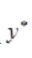＝-1。
所以原方程的通解为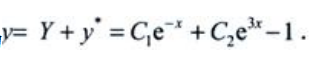（C₁，C₂为任意常数）

2、求曲线y＝x²在点（a，a²）（a＜1）的一条切线，使由该切线与x＝0、x＝1和y＝x²所围图形的面积最小。

答 案：解：设所求切线的切点为（a，b），见下图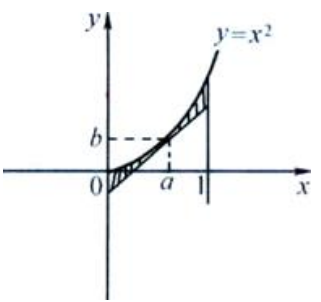，则b＝a²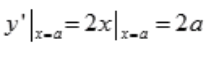，，切线方程为y－b＝2a（x－a），y＝2ax－2a²＋b＝2ax－a²。设对应图形面积为A，则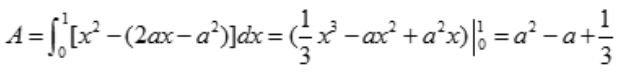
令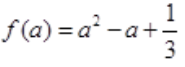，则，令。当a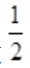＜时，f'(a)＜0；当a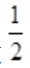＞时，f'(a)＞0，故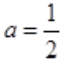为f(a)的最小值点，切线方程为：y＝x－。

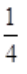3、设f（x，y）为连续函数，交换二次积分的积分次序。

答 案：解：由题设知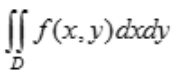中积分区域的图形应满足1≤x≤e，0≤y≤lnx，因此积分区域的图形见下图中阴影部分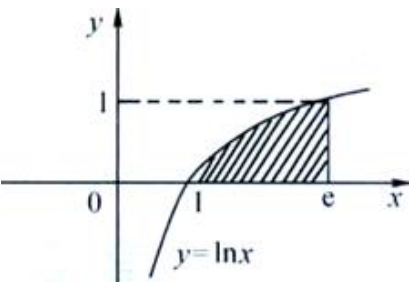．由y＝lnx，有x＝e^y。所以。

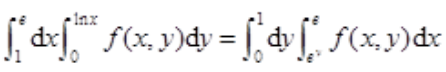填空题

1、级数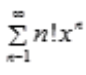的收敛半径是（）。

答 案：

解 析：

2、设函数z＝f（x，y）可微，（x₀，y₀）为其极值点，则（）。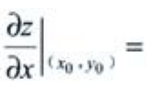

答 案：

解 析：由二元函数极值的必要条件可知，若点（x₀，y₀）为z＝f（x，y）的极值点，且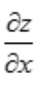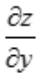，在点（x₀，y₀）处存在，则必有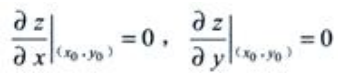，由于z＝f（x，y）可微，则偏导数必定存在，因此有。

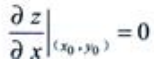3、设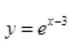，则dy＝（）。

答 案：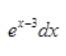

解 析：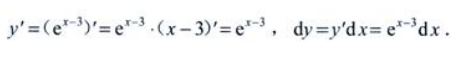

简答题

1、求微分方程y”-y’-2y=3e^x的通解。  

答 案：  

解 析：本题考查的知识点为求解二阶线性常系数非齐次微分方程。