单选题
1、点(2,4)关于直线y=x的对称点的坐标为（）
答 案：A
解 析：点(2,4) 关于直线y=x对称的点为(4,2)
2、已知函数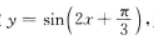
，则下列命题中正确的是（ ）
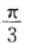得到的
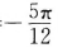成轴对称图形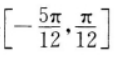
答 案：C
解 析：显然它不是奇函数，不能认为含有“sin”符号的函数就是奇函数，故A项错误．图象的平移要看函数式中的自变量z的变化情况．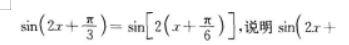
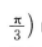的图象是把 sin2x 的图象向左平
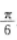。一般说来,sin(ωx+y)的图象是将sinωx 的图象沿x轴正方向平移了
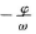而得到的,故B项错误,过函数y=sinx的每一个最大值点或最小值点(即使sinx=1或-1的点)作x轴的垂线,都是其函数图象的对称轴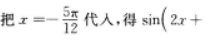
【考点指要】本题考查了三角函数的奇偶性、单调性以及图象的平移与对称轴，对三角函数的性质进行了较全面的考查．
3、△ABC中，已知AC=12，∠A=30°，∠B=120°，则BC=（）
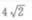
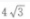
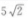
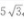
答 案：B
4、设M=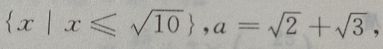
那么（）
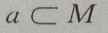
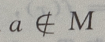
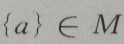
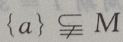
答 案：D
解 析：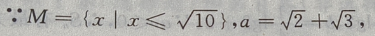
M是集合，a为元素，{a}为集合，元素与集合的关系是
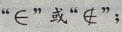集合与集合的关系是
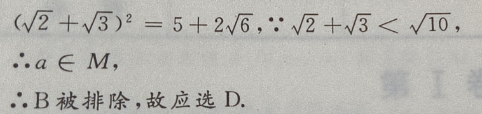
主观题
1、已知a-a-1=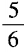
，求a3-a-3的值。
答 案：
2、若双曲线
的两条准线将两个焦点的连线分成三等分,求双曲线的离心率。
答 案：设双曲线的半焦距为c，则双曲线
【考点指要】本题要求根据双曲线的焦距、离心率、准线方程三者之间的关系进行计算，属较容易题，在成人高考中常见．
3、在△ABC中，已知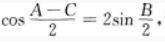
证明a，b，c成等差数列。
答 案：
考点 本题主要考查三角函数的恒等变换以及积化和差公式的应用，积化和差有一定难度，请考生注意．
4、已知x+x-1=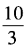
，求x2+x-2的值。
答 案：由已知，得
填空题
1、平面内有10个点，任何三点都不在同一直线上，问能连成______条不同的直线。
答 案：45
2、若6sinαcosα=1，则tanα的值等于______。
答 案：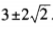
解 析：由已知，sin2α=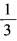
。由于
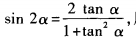所以 
