单选题
1、过圆x2+y2-2x-8=0的圆心,且与直线x+2y=0垂直的直线方程是()
- A:2x-y+2=0
- B:x+2y-1=0
- C:2x+y-2=0
- D:2x-y-2=0
答 案:D
解 析:因为x2+y2-2x-8=0的标准方程为(x-1)2+y2=9,所以圆心为(1,0).易知直线x+2y=0的斜率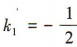 .设过圆心(1,0)且与直线x+2y=0垂直的直线的斜率为k2,则k1·k2,=-1,所以k2= 2,所以所求直线的方程为y=2(x-1),即2x-y-2=0.
.设过圆心(1,0)且与直线x+2y=0垂直的直线的斜率为k2,则k1·k2,=-1,所以k2= 2,所以所求直线的方程为y=2(x-1),即2x-y-2=0.
2、已知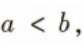 则下列各式中,错误的是()
则下列各式中,错误的是()
- A:
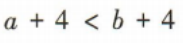
- B:
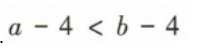
- C:
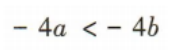
- D:

答 案:C
解 析:
3、圆心在y轴上,半径为1,且过点(1,2)的圆的方程为()
- A:x²+(y-2)²=1
- B:x²+(y+2)²=1
- C:(x-1)²+(y-3)²=1
- D:(x-2)²+(y-3)²=1
答 案:A
解 析:由题意可设圆的圆心坐标为(0,b).由题意得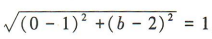 ,解得b=2,所以该圆的方程为x²+(y-2)²=1.
,解得b=2,所以该圆的方程为x²+(y-2)²=1.
主观题
1、已知
答 案:方法一:矢量图表示法 矢量图表示法如图所示。
 方法二:矢量表示法
方法二:矢量表示法
解 析:


填空题
1、若(x-1)n的展开式中x2的系数是-10,则n的值为()
答 案:5
解 析:因为(x-1)n的展开式中x2的系数是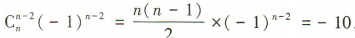 ,所以n= 5.
,所以n= 5.
2、如图,在矩形ABCD中,AB=2AD=2,沿对角线AC将 翻折,使二面角D-AC-B成直二面角,连接BD,则BD的长为()
翻折,使二面角D-AC-B成直二面角,连接BD,则BD的长为() 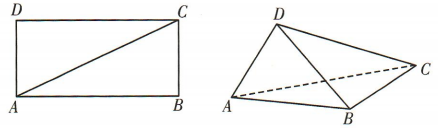
答 案: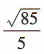
解 析: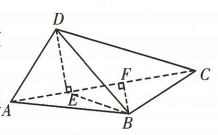 如图,过点D作
如图,过点D作 于点E,过点B作
于点E,过点B作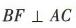 于点F,连接BE.由题意知
于点F,连接BE.由题意知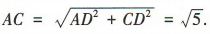 易得
易得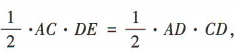 解得
解得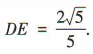 同理
同理
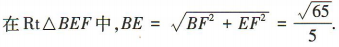 ∵D-AC-B是直二面角,
∵D-AC-B是直二面角,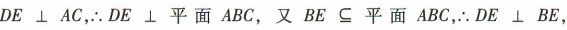

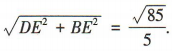
3、在△ABC中,内角A,B,C的对边分别为a,b,c,且c=3,sinB=2sinA,且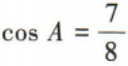 b≠c
(1)求b的值;
(2)求△ABC的面积.
b≠c
(1)求b的值;
(2)求△ABC的面积.
答 案: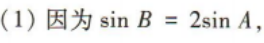
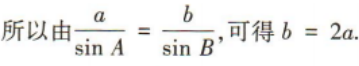
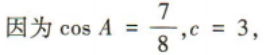


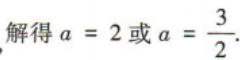
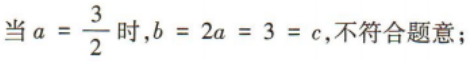
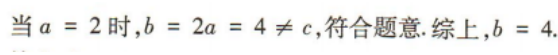

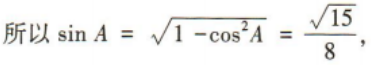

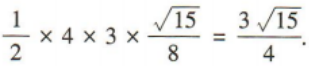
简答题
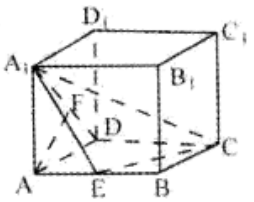
1、如图:在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=√6 ,E,F分别为AB和A1D中点.
(1)求证:AF//平面A1EC .
(2)求A1C与底面ABCD所成角的正切值.
答 案:(1)证: 取A1C的中点0,连接OF,OE
在△A1CD中,F,O分别为AD,A1C的中点.
故FO//DC,且FO=1/2DC
则FO//AB,FO=1/2AB=AE,
得四边形AEOF是平行四边形,AF//OE
故AF//平面A1 EC
(2)解:连接AC,AA1⊥平面ABCD
在Rt△A1AC中,tan∠A1CA= 因此角的正切值为
因此角的正切值为