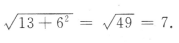单选题
1、一部电影在4个单位轮映，每一单位放映一场，轮映次序有（）。
答 案：C
2、中心在坐标原点，对称轴为坐标轴，且一个顶点（3，0），虚轴长为8的双曲线方程是（）
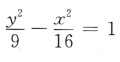
答 案：B
解 析：双曲线有一个顶点为(3,0)，因此所求双曲线的实轴在x轴上，可排除A、C选项，又由于虚轴长为8，故b=4，即b2=16，故双曲线方程为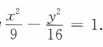
3、已知2a=3，2b=6，2C=12，则（）.
答 案：C
解 析：由已知，2a·2c=36，即2a+c=36。又（2b）2=62，22b=36，则22b=2a+c，2b=a+c选C。
4、若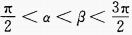
，则必有（）。
答 案：A
解 析：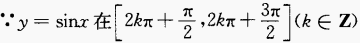
是函数，故当
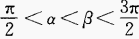时，
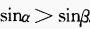
主观题
1、已知关于x的二次方程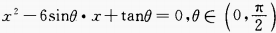
的两根相等，求sinθ+cosθ的值。
答 案：
2、求函数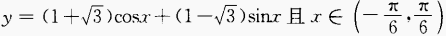
上的最大值以及取得这个最大值的x。
答 案：.1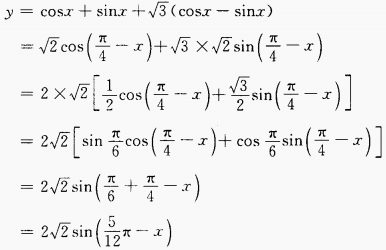 
函数取最大值，即y最大值=。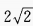
3、已知函数f(x)=(x-4)(x2-a) （I）求f"(x)； (Ⅱ)若f"(-1)=8，求f(x)在区间[0，4]的最大值与最小值
答 案：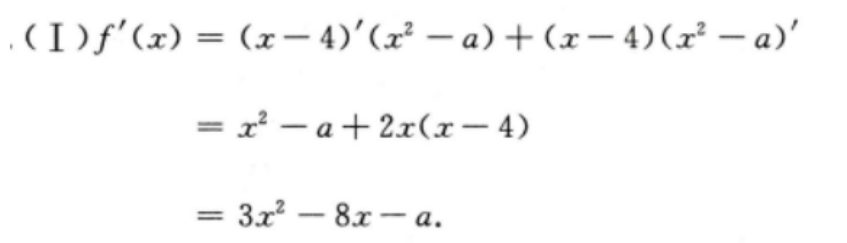
4、已知x+x-1=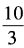
，求x2+x-2的值。
答 案：由已知，得
填空题
1、sin210°+sin220°+sin240°+sin250°+sin270°+sin280=______。
答 案：3
解 析：由互为余角的余函数值相等得 原式=(sin210°+cos210°)+(sin220°+cos220°)+(sin240+cos240)=1+1+1=3
2、长方体的长、宽、高分别为2,3,6，则该长方体的对角线长为（）
答 案：7
解 析：由题可知长方体的底面的对角线长为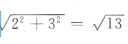
，则在由高、底面对角线、长方体的对角线组成的三角形中，长方体的对角线长为
