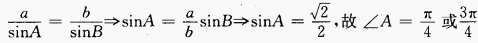单选题
1、若函数f（x）是奇函数，则函数
的奇偶性是（）。
答 案：A
解 析：∵f(x)是奇函数
∴f(-x)=-f(x)
∵F(x)=f(x)·(-cosx)=-f(x)cosx
∴F(-x)=-f(-x)cos(-x)= f(x)cosx =-F(x)
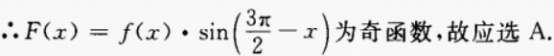注：由此可知，奇函数×偶函数为奇函数；奇函数×奇函数为偶函数；偶函数×偶函数为偶函数。
2、设log2x=a，则log2(2x2)=（）。
答 案：D
解 析：本题主要考查的知识点为对数函数的性质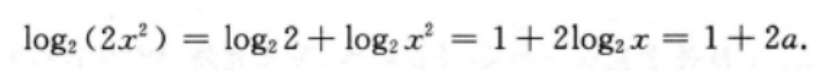
3、已知
，则sin2α=（）
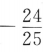
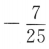
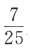
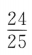
答 案：D
解 析：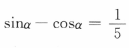
两边平方得
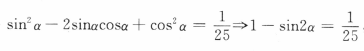，故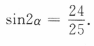
4、已知x+x-1=2cos40°，则x4+x-4=（）.
答 案：B
解 析：由已知得(x+x-1)2=(2 cos 40°)2,x2+2+x-2=4cos240°,x2+x-2=2(2 cos240°-1)=2cos 80°同样可得x4+x-4=2 cos 160°=-2 cos 20°
主观题
1、试证明下列各题
（1）
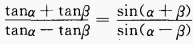
（2）
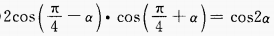
答 案：（1）化正切为正、余弦，通分即可得证。 （2）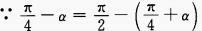
2、求（1+tan10°）（1+tan35°）的值。
答 案：原式=1+tan10°+tan35°+tan10°·tan35°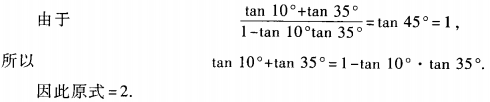
3、已知函数f(x)=(x-4)(x2-a) （I）求f"(x)； (Ⅱ)若f"(-1)=8，求f(x)在区间[0，4]的最大值与最小值
答 案：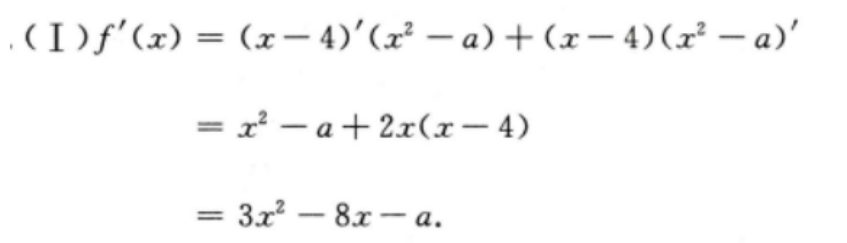
4、已知空间四边形OABC，OB=OC且∠AOB=∠AOC=θ（如图）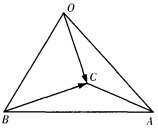
。求证：OA⊥BC。
答 案：
填空题
1、曲线y=在点(1，1)处的切线方程是______。
答 案：2x+y-3=0
解 析：本题主要考查的知识点为切线方程
由题意，该切线斜率，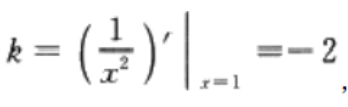
又过点(1，1)，所以切线方程为y-1=-2(x-1)
2、在△ABC中，a=2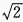，b=
，∠B=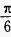
，则∠A=______。
答 案：
解 析：
