单选题
1、（2-3i）2=（）
答 案：D
解 析：
2、若函数f（x）是奇函数，则函数
的奇偶性是（）。
答 案：A
解 析：∵f(x)是奇函数
∴f(-x)=-f(x)
∵F(x)=f(x)·(-cosx)=-f(x)cosx
∴F(-x)=-f(-x)cos(-x)= f(x)cosx =-F(x)
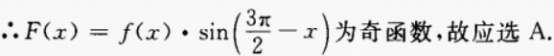注：由此可知，奇函数×偶函数为奇函数；奇函数×奇函数为偶函数；偶函数×偶函数为偶函数。
3、下列各式中，不成立的是（）。
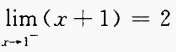
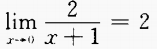
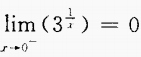
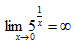
答 案：D
解 析：可用排除法，A、B、C均成立。
4、若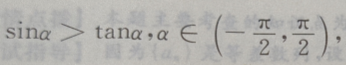
则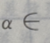
（）
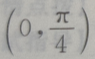
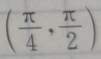
答 案：B
解 析：首先做出单位圆,然后根据问题的约束条件,利用三角函数线找出满足条件的a角取值范围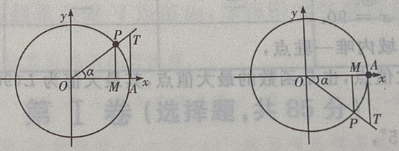 
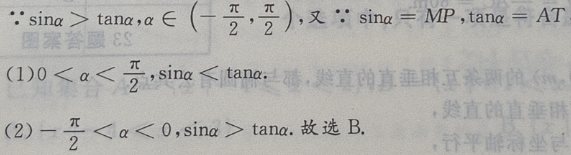
主观题
1、（1）已知tanα=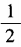
，求cot2α的值； （2）已知tan2α=1，求tanα的值。
答 案：（1）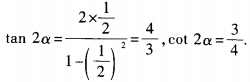
（2）由已知，得
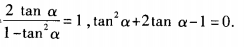解关于tanα的一元二次方程，得tanα=
2、函数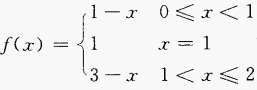
在其定义域上是否连续？作出f（x）的图形。
答 案：f（x）的定义域为[0，2] 当0≤x<1时f（x）=1-x是连续的 当1
3、已知x+x-1=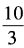
，求x2+x-2的值。
答 案：由已知，得
4、设
分别讨论x→0及x→1时f（x）的极限是否存在？
答 案：
∴f（x）在x=0处极限不存在 同理f（x）在x=1处极限存在
填空题
1、一个问题在1小时内，甲能独立解决的概率是0.5，乙能独立解决的概率是0.4，两人在1小时内解决问题的概率是______。
答 案：0.7
解 析：设事件A为两人在1小时内解决问题，即1小时内至少有一人能解决问题，事件B为甲在1小时内解决问题，事件C为乙在1小时内解决问题，事件B、C是相互独立事件，事件A的对立事件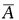
互为在1小时内两个人都没有解决问题，所以 P（A）=1-P（
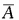）=1-P（
·
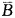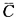）=1-P（
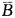）·P（
）
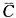=1-（1-0.5）×（1-0.4）=1-（0.5×0.6）=1-0.3=0.7
2、函数y=2cosx-cos2x（x∈R）的最大值为______。
答 案：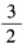
解 析：
