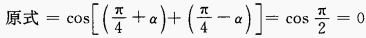单选题
1、已知向量a=(3,4),向量 b=(0,-2),则cos的值为（）
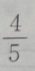
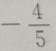
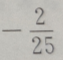
答 案：B
解 析：求cos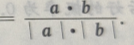
a·b=(3,4)·(0,-2)=3×0+4×(-2)=8,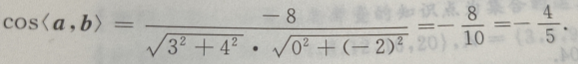
2、i为虚数单位,則i•i2•i3•i4•i5的值为（）。
答 案：D
解 析：i•i2•i3•i4•i5=i1+2+3+4+5=i15=-i
3、设F1和F2为双曲线的两焦点,点P在双曲线上,则||PF2|-|PF2||=（）。
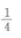
答 案：A
解 析：由题意有a2=4.a=2,由双曲线的定义,可知||PF2|-|PF2||=2a=4.(答案为A)
4、若甲：x>1,乙：
则
答 案：D
解 析：
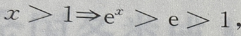而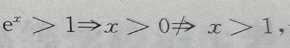
故甲是乙的充分条件，但不是必要条件
主观题
1、已知数列{an}中，a1=2，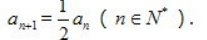
（Ⅰ）求数列{an}的通项公式;
（Ⅱ）求数列{an}前5项的和 S5
答 案：解：
2、已知一组数据9.9；10.3；9.8；10.1；10.4；10；9.8；9.7，计算这组数据的方差。
答 案：
3、已知等差数列前n项和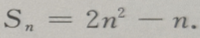
（Ⅰ）求这个数列的通项公式;（Ⅱ）求数列第六项到第十项的和
答 案：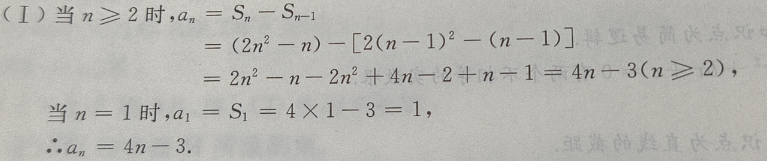
4、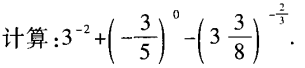
答 案：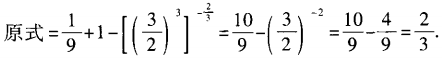
填空题
1、ABCD是正方形，E是AB的中点，如将△DAE和△CBE分别沿虚线DE、CE折起，使AE与BE重合如图
，设A与B重合后的点为P，则面PCD与面ECD所成的二面角为______度，PE与面ECD成______度。
答 案：二面角为30°，PE与面ECS成60角°
解 析：（1）求面PCD与面ECD所成的二面角为多少度，就是要求出由平面PCD与平面ECD所组成的二面角的平面角，其中画出二面角的平面角是关键，因为二面角确定以后，二面角的平面角很容易画出（由二面角的平面角的定义）。求角度时，常用到勾股定理、正弦定理、余弦定理、兰垂线定理和逆定理。 （2）求PE与面ECD成多少度，就是求直线与平面所成的角是多少度。首先要找出平面的一条斜线（直线PE）和斜线的射影，斜线和射影所成的锐角，就是直线PE和平面ECD所成的角，再求出角度。 设CD的中点为F，练PF，EF
∵PC=PD，EC=ED.
∴PF⊥CD，EF⊥CD（三垂线定理）
∠PFE是二面角P-CD-E的平面角
∵PE⊥PC，PE⊥CD.
∴PE⊥平面PCD，又PF在平面PCD内
∴PE⊥PF
设正方形边长为1（如图）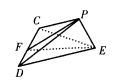
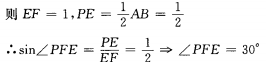故面PCD与面ECD所成的二面角为30°，PE与面ECS成60角°。
2、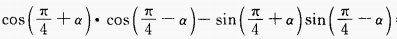
=______。
答 案：0
解 析：
