单选题
1、从13名学生中选出2人担任正副班长，不同的选举结果共有（）。
答 案：C
2、直线2x-y+7=0,与圆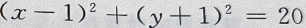
的位置关系是（）
答 案：C
解 析：易知圆心坐标（1，-1），圆心到直线2x-y+7=0的距离d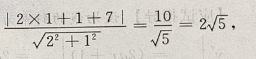
∵圆的半径
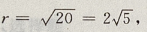∴d=r，∴直线与圆相切
3、△ABC中，已知AC=12，∠A=30°，∠B=120°，则BC=（）
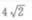
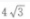
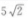
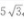
答 案：B
4、如果点（2，一4)在一个反比例函数的图像上，那么下列四个点中也在该图像上的是（）
答 案：A
解 析：设反比例函数为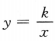
，点（2,-4)在反比例函数的图像上，因此有
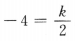，解得k=-8，故反比例函数
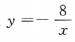，当x=-2时，y=4，故选A在该图像上.
主观题
1、已知lg2=a，lg3=b，求lg0.15关于a，b的表达式。
答 案：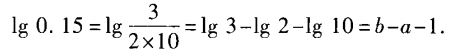
2、设3a=5b=15，求a-1+b-1的值。
答 案：由3a=15，得a=log315；又由5b=15，得b=log515。 因此a-1+b-1=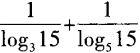
=log153+log155=1。
解 析：过程中应用了换底公式的推论，即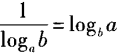
3、一艘渔船在航行中遇险，发出警报，在遇险地点西南10海里处有一艘货轮，接收到报时，发现遇险渔船正以9海里/小时的速度与沿南偏东75°方向向某小岛靠近，如果要在40分内将这艘渔船救出，求货轮航行的方向和速度。
答 案：货轮沿东偏北21.8°的方向，以21海里/小时的船速航行。
4、已知三角形的三边边长组成公差为1的等差数列，且最大角是最小角的二倍，求三边之长。
答 案：三角形的三边边长分别为4，5，6。
填空题
1、设
则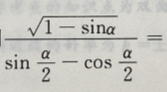
答 案：-1
解 析：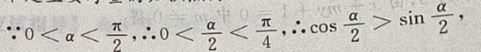
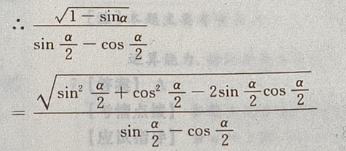
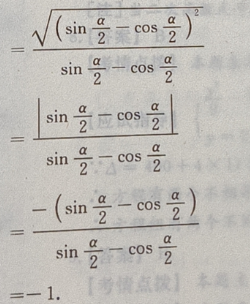
2、袋中装有3个白球，2个红球，从中任取2个球，取到2个都是红球的概率是______。
答 案：
解 析：
